Understanding Latent Dirichlet Allocation (1) Backgrounds
Latent Dirichlet allocation (LDA) is a three-level bayesian hierarchical model that is frequently used for topic modelling and document classification. First proposed to infer population structure from genotype data, LDA not only allows to represent words as mixtures of topics, but to represent documents as a mixture of words, which makes it a powerful generative probabilistic model.
This article is the first part of the series “Understanding Latent Dirichlet Allocation”.
In this series of articles, I would like to explain backgrounds and model structure, and to implement it from scratch with numpy.
Before we get into the detail, I would like to mention and define terms that will be used frequently hereafter.
Tokens (or words) are grammatical and/or semantic unit of language, usually separated with each other in a sentence by a space1. Documents (or sentence) are collection of words in specific orders. A Corpus is a collection of documents. Vocabulary is the set of all words in a corpus.
Topics are latent structure of documents that cannot be explicitly observed, but can be represented as sets of similar words. Bayesian hierarchical model is a statistical model that sequentially conditioning random variables and their parameters with higher-order hyperparameters. Topic modelling is a process to identify such structure with statistically modeling the documents. Generative models, unlike discriminative models, learn the underlying distributional structure so that it can generate the random data.
While the terms might not be familiar to some, it will become clear with real model description in the next post.
TF-IDF matrix
In the beginning of embedding documents to numeric vectors, TF-IDF matrix was frequently used. Term frequency-inverse document frequency (TF-IDF) is a simple yet useful index to quickly convert documents into vectors. TF-IDF is calculated as follows. First, term frequency (TF) is defined for each words in vocabulary ($v_i$) and documents($\mathbf{w}_d$).
\[\text{TF}(v_i, \mathbf{w}_d) = (\text{# of occurence of $v_i$ in } \mathbf{w}_d)\]This is sometimes refered to as raw term frequency.
Inverse document frequency (IDF) is defined as an adjusted inverse of document frequency (DF).
\[\text{DF}(v_i) = (\text{# of documents contaning } v_i) \\ \text{IDF}(v_i, D) = \log\left(\frac{\text{# of documents in } D}{1 + \text{DF}(v_i)}\right)\]Finally, TF-IDF is a product of TF and IDF.
\[\text{TF-IDF}(v_i, \mathbf{w}_d, D) = \text{TF}(v_i, \mathbf{w}_d) \cdot \text{IDF}(v_i, D)\]Computing TF-IDF for all documents and words in a corpus yields a document-term matrix. Row vectors of the matrix can be viewed as document embeddings.
Latent Semantic Analysis
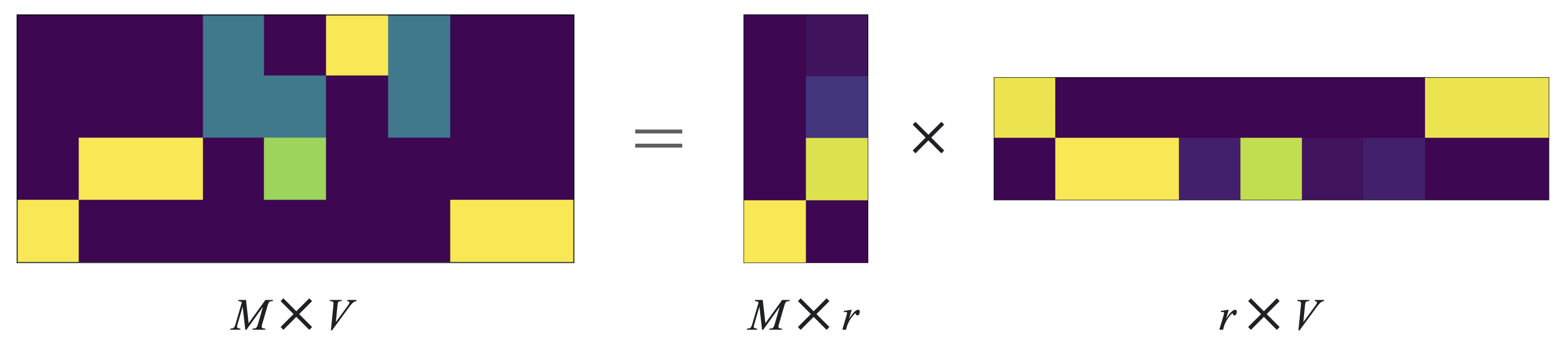
TF-IDF LSA is just a singular value decomposition of TF-IDF matrix. The rationale is to capture lower-dimensional latent structure behind terms and documents. While TF-IDF reveals provides information, the matrix is sparse and the dimension of each word vector is as large as the size of vocabulary (usually in the order of millions). By applying $r$-truncated singular value decomposition to TF-IDF matrix of size $M\times V$ where $M$ is the size of corpus (total number of documents) and $V$ is the size of vocabulary, we get two matrices of size $M\times r$ and $r \times V$. The first matrix can be used as a document embedding, and the second as a word embedding.
Probabilistic LSA
pLSA is an attempt to model the latent topics as mixture distributions. While LSA is an exact decomposition of TF-IDF matrix, pLSA poses distributional assumptions to word and document generation and finds parameters that best explain it. In this model, words are realized random variables that follow mixtures of multinomial distributions and such mixtures can be veiwed as topics.

It was a paradigm shift to use hierarchical model for topic modelling, but pLSA has weakness: While pLSA is a generative model for words, it is not generative in terms of (unseen) documents. Hence as the number of documents in the training set grows, the number of parameters of the model linearly grows as well which makes it non-scalable and vulnerable to overfitting.
Latent Dirichlet Allocation
LDA solves the exact problem that pLSA had: it additionally models documents as mixture distribution of topics starting from the meaning behind bag-of-words assumption.
Under BoW assumption, order of words in a document, and in extension, order of documents in a corpus is disregarded. To put it in a statistical statement, BoW assumes that words and documents are exchangeable. de Finetti’s theorem states that the distribution of a sequence of exchangeable random variables can be represented as a mixture (weighted mean) of distributions of IID random variables. Thus a desired generative model has not only mixture representations of words, but also of documents.
The result of consideration is LDA, Details of which will be covered in the next post.
References
- Blei, Ng, Jordan. 2003. Latent Dirichlet Allocation. Journal of Machine Learning Research. 3 (4–5): 993–1022.
-
While tokens are actually processed words by stemming/lemmatizing processes, I will not separate the two here. ↩