Convolutional Neural Network (CNN) 이해하기
지난 글 시리즈에서는 뉴럴넷 중 가장 단순한 형태인 MLP, 즉 dense (fully connected) layer만을 사용하는 뉴럴넷과 이를 학습시키는 방법에 대해서 살펴보았다. MLP를 사용하면 효과적으로 비선형 함수를 모사할 수 있었고 이 덕분에 기존의 선형함수 기반 모형에 비해 훌륭한 성능을 낼 수 있었다.
그러나 실제 데이터를 올바르게 분류하거나 회귀할 때에는 이보다는 복잡한 구조가 필요한 경우가 있다. 다음의 몇 가지 상황을 생각해보자.
1) MLP에서는 별도의 feature engineering 없이 raw feature를 곧바로 입력층에 넣었었다. 붓꽃 데이터, 또는 데이터의 차원이 크지 않은 경우에는 raw feature를 전부 사용해도 모형의 파라미터 수가 크지 않았기 때문에 학습 과정에서 문제가 생기지 않았고 성능도 좋았지만, 이미지와 같은 데이터에서는 문제가 달라진다.
이미지 데이터를 예시로 들어보자. 가로 48픽셀, 세로 48픽셀의 컬러(RGB) 이미지 데이터를 생각해보자. 이 이미지의 각각의 픽셀을 하나의 feature로 사용해서 MLP의 입력층에 넣을 수 있을 것이다. 이렇게 feature engineering 없이 각 픽셀의 raw value를 전부 입력으로 넣는다면, 뉴럴넷이 감당해야 하는 feature 차원수는 $48 \times 48 \times 3 = 6912$가 된다. 겨우 가로세로 48픽셀밖에 안되는 저화질 이미지였는데도 feature 차원이 7000에 달한다. Feature 갯수가 이렇게 많아지게 되면 컴퓨팅 속도가 저하되고 오버피팅의 위험이 생길 수 있다.
2) MLP에서는 각 샘플이 등장한 맥락을 고려하지 않았다. 즉, 샘플들이 정렬되어 있는 순서가 중요하지 않았다. 그러나 주식 일별 종가, 문장 속 단어와 같은 데이터에서는 각 샘플의 앞 뒤로 어떤 샘플들이 있었는지의 정보(‘문맥’)도 중요하다. 이 경우엔 MLP만으로는 충분히 좋은 성능을 발휘할 수 없다.
이번 시리즈에서는 전통적인 dense layer 외에 이미지 등의 데이터를 처리하기 위해 새로이 고안된 뉴럴넷의 레이어에 대해서 살펴보고자 한다. 그 시작은 convolutional neural network (CNN; ConvNet)을 구성하는 레이어들이다.
Convolutional (CONV) layer
앞의 예시에서 이미지의 각 픽셀을 그대로 feature로 사용하는 것은 좋지 않은 방법이라는 것을 언급했었다. 대신 각 이미지로부터 독특한 특성만을 뽑아내어 feature로 사용한다면 더 좋은 성능을 낼 수 있을 것이다. 이 과정을 feature extraction이라고 하고, 이미지에서 feature extractor로 동작하는 레이어가 바로 convolutional layer이다.
Convolutional layer는 두 가지 가정을 전제로 한다.
- Local connectivity: 이전 레이어의 모든 뉴런과 연결되는 MLP에서와는 달리 CONV layer는 이전 레이어의 뉴런 중 일부와만 연결된다. 즉 이미지의 모든 픽셀과 연결되는 대신 이미지 중 일부분의 픽셀과만 연결된다.
- Spatial invariance: 이미지의 한 부분의 데이터 분포는 다른 부분에서의 데이터 분포와 다르지 않다. 즉, 이미지의 분포적인 특성은 어느 부위에서든 동일하다고 가정하는 것이다.
Dense layer에서 각 입력 샘플을 1차원의 벡터 데이터로 보았다면, Convolutional layer는 입력 샘플을 3차원의 텐서(Tensor) 데이터로 인식한다. Convolutional layer는 입력 3차원 데이터를 적절히 변형해서 또다른 3차원 데이터를 출력한다.
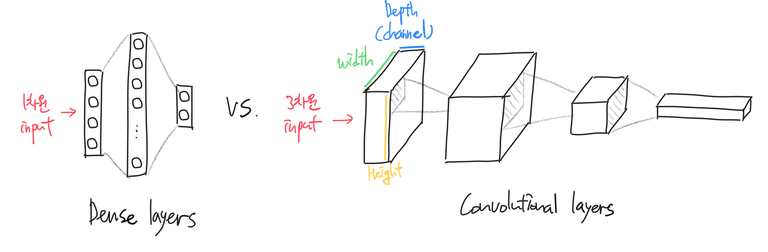
Convolutional layer가 하는 일을 자세히 살펴보자.
- 먼저 이미지에서 특징적인 부분을 추출하는 데에 사용될 필터(또는 커널)가 정의되어야 한다. 필터 크기는 이미지 크기보다 작거나 같다. 필터는 인풋 이미지를 시작부터 끝까지 차례차례 훑으면서(마치 sliding window처럼) 이미지 픽셀 값에 필터 값을 곱해 더한 값을 출력한다.
- 필터가 이미지를 얼마나 자세히 훑으면서 지나갈지를 결정해야한다. 이것을 stride라고 한다. Stride가 1로 정의된 경우, 필터는 이미지 위를 한 번에 한 픽셀씩 이동하면서 자세히 훑는다. Stride가 10으로 정의된 경우, 필터는 이미지 위를 한 번에 10픽셀씩 이동하면서 대충 훑는다. (가로방향 stride와 세로방향 stride를 다르게 설정할 수도 있다)
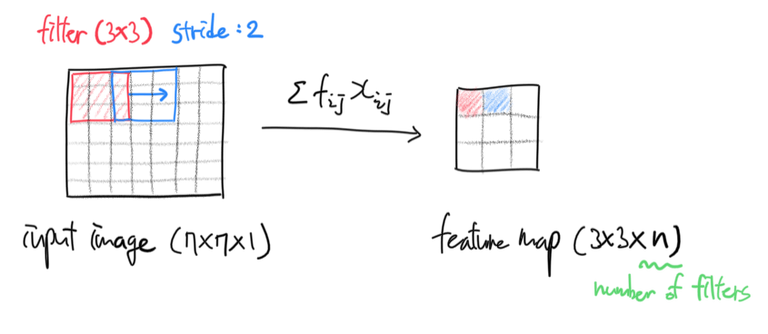
$f_{ij}$는 필터의 $i$행 $j$열 값, $x_{ij}$는 인풋 이미지의 $i$행 $j$열 값이다.
즉 convolutional layer는 필터를 일정 간격씩 이미지 위에서 이동시키면서 필터 값을 이미지 픽셀값에 곱하여 더한 값을 출력한다. 출력된 feature map의 픽셀 하나는 인풋 이미지 중 3x3만큼의 정보를 바탕으로 결정된 값이다. 이 feature map의 receptive field 크기는 3x3이 된다는 뜻이다. 인풋 이미지 중 3x3만큼을 ‘보고’ Feature map의 픽셀 하나의 값을 계산했다는 의미다.
애니메이션으로 살펴보면 이해가 쉽다. 파란색은 인풋 이미지, 초록색은 필터이다.
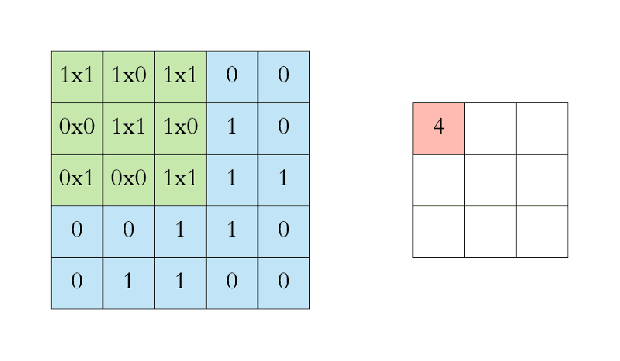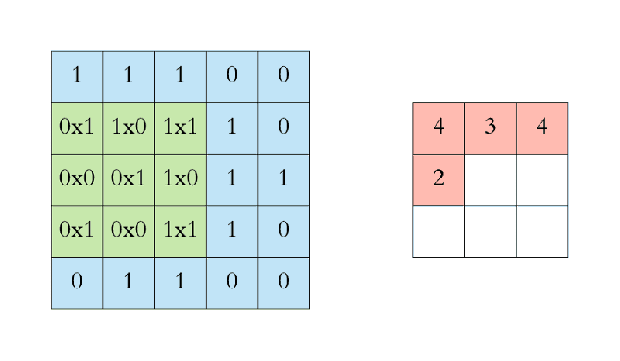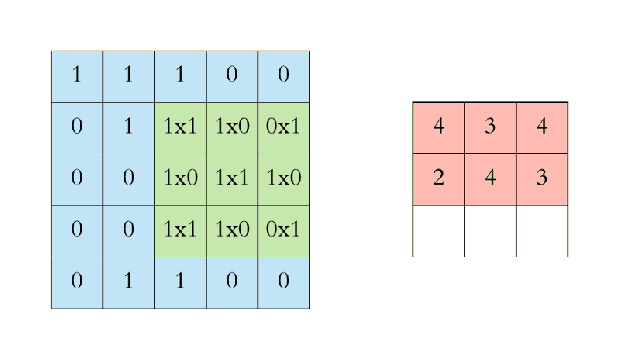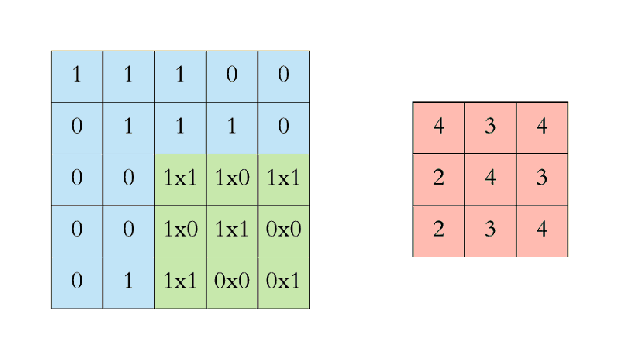
초록색 필터가 이미지를 한 칸씩(stride=1) 돌아다니면서 곱의 합을 출력하는 것을 볼 수 있다. 이렇게 출력된 값(convolved feature 또는 feature map; 붉은색)을 추출된 이미지의 특징이라고 생각하여 feature로 사용할 수 있다.
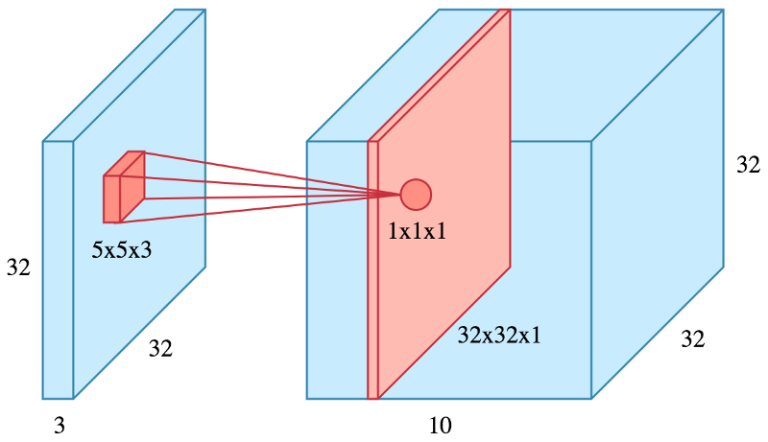
필터 하나 당 하나의 feature map이 만들어지므로, 필터 $n$개를 사용하는 CONV layer의 출력은 depth=$n$을 갖는 텐서가 된다. 만약 32x32짜리 컬러(depth=3) 이미지 하나가 필터 10개를 사용하는 CONV layer를 통과하면 그 출력 depth는 10이 된다.
수학/신호처리학에서의 cross-correlation
주의해야할 것은 수학에서 정의하는 convolution 연산과는 다른 연산이라는 것이다. 오히려 뉴럴넷에서의 convolution 연산은 수학/신호처리에서의 cross-correlation과 같다.
신호처리에서 cross-correlation은 두 신호간의 유사성을 잴 때에 사용되는 연산이라고 한다. 때문에 뉴럴넷에서의 convolution도 convolution filter와 input image 사이의 유사성을 측정해서 출력하는 연산이라고 생각할 수 있다. 필터와 이미지의 패턴이 유사하다면 절대값이 큰 값을, 그렇지 않다면 작은 값을 반환하는 것이다.
예를 들어, 아래처럼 우상에서 좌하로 향하는 사선 모양의 convolution filter는 이미지 내에서 사선 모양이 있는 부분(주로 이미지의 윤곽선)을 보면 큰 값을 출력한다. 아래 돌고래 이미지에서 우상좌하 사선 모양의 윤곽선이 도드라지게 추출된 것을 확인할 수 있다.


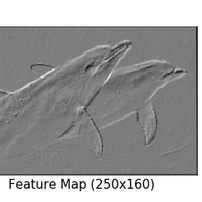
실제 ConvNet에서는 필터를 우리가 직접 정해주지 않고 알고리즘이 데이터를 바탕으로 문제 해결에 적합한 형태가 되도록 학습해나간다.
Zero padding
이미지에 필터를 적용할 때, 아무리 촘촘히(stride=1) convolution을 해도 출력된 feature map의 가로세로 크기는 원본 이미지에 비해 반드시 작아질 수 밖에 없다. 원본 이미지와 가로세로 크기가 같은 feature map을 얻기 위해서는 필터를 적용하기 전에 입력 이미지에 처리를 해주어야 한다.
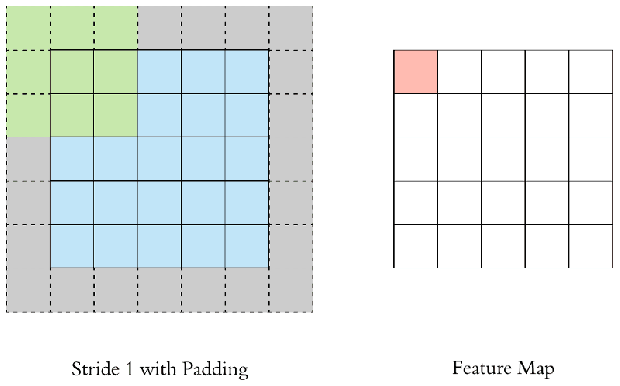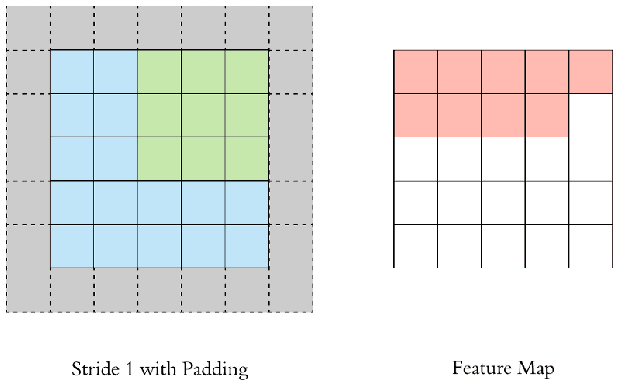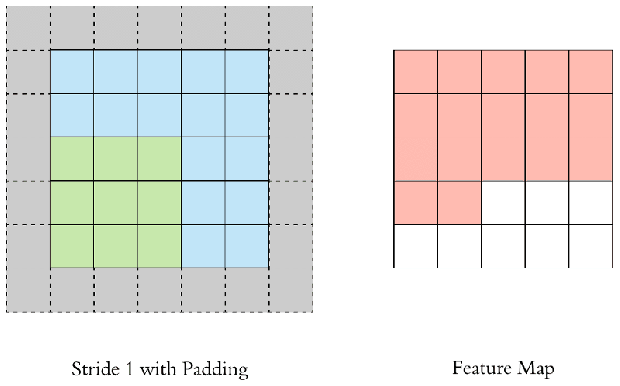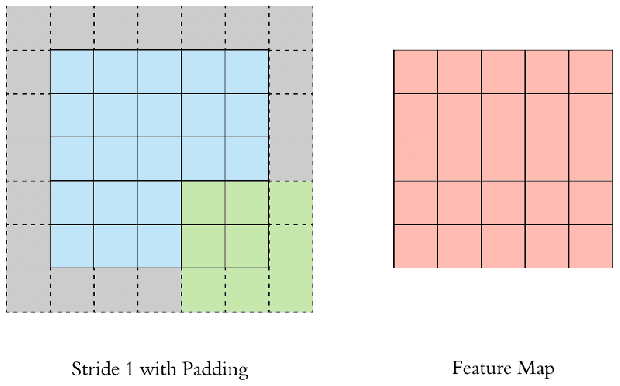
단순하고도 널리 사용되는 방법이 바로 zero padding, 즉 원본 이미지의 상하좌우를 0값으로 둘러싸는(padding) 방법이다. 아무 정보가 없는 0값으로 이미지를 패딩함으로써 feature map의 가로세로 크기를 인풋과 같게 유지하면서 convolution layer를 깊게 쌓을 수 있다.
ReLU layer
CONV layer를 통해서 이미지로부터 추출한 feature map에서 양의 값만을 활성화시키는 레이어다. ReLU layer에서는 feature map에서 특히나 두드러지는 특징을 다시 추출한다.
사실 별도의 layer라고 칭하기는 좀 뭣하고, CONV layer의 activation function으로 ReLU를 사용한 것이라 이해하면 쉽다.
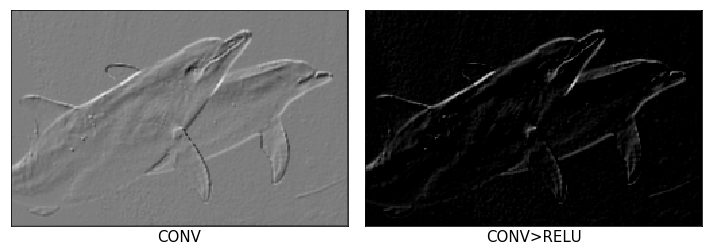
ReLU activation 적용 후 우상좌하 사선 모양의 윤곽선이 매우 잘 추출되었다.
POOL layer
수많은 이미지를 처리하는 과정에서 필연적으로 맞딱뜨릴 수 밖에 없는 것이 바로 메모리 문제다. 특히나 CONV layer는 원본 이미지의 가로세로 크기를 유지하면서 depth를 수백~수천 수준으로 키우기 때문에 메모리를 많이 먹는 레이어다. 이때문에 이미지와 feature map의 가로세로 크기를, 그 특징은 유지하되 적절한 수준으로 다운샘플링하여 메모리를 절약할 필요가 있다. 다운샘플링 방법 중 ConvNet에서는 pooling을 사용한다.
가장 빈번히 사용되는 풀링은 max pooling이다. Max pooling은 pool region 내에서 가장 수치가 큰 위치의 값만을 가져온다.
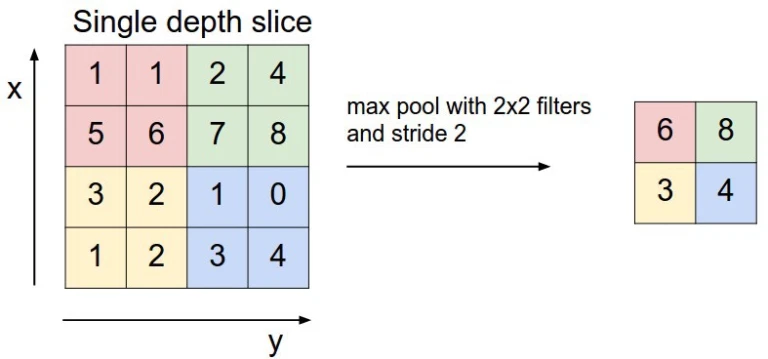
2x2의 pool size, stride 2로 max pooling을 적용한 모습이다. 2x2의 pool region 내에서 가장 수치가 큰 값만을 샘플링한 것을 볼 수 있다.
Weakly-supervised localization 등의 문제를 해결할 때에는 average pooling을 사용하기도 한다. Average pooling은 해당 pool region 내의 모든 값을 평균내어 가져온다.
돌고래 이미지의 예시에 2x2 max pooling (stride 2)을 적용한 결과, 아래와 같이 feature map의 특징은 유지하면서 이미지 크기를 1/4로 축소할 수 있었다.

ConvNet의 일반적인 구조
일반적으로 ConvNet의 구조는 다음과 같이 표현할 수 있다.
\[\{(\text{CONV} + \text{ReLU}) \times n + \text{POOL} \} \times m + (\text{Dense} \times k)\]여기서 CONV + RELU + POOL은 feature extractor 역할을 하고 Dense layer는 classifier 또는 regressor 역할을 한다. 이미지 분류 문제를 예시로 들자면, CONV + RELU + POOL은 인풋 이미지로부터 분류에 사용할만한 특징적인 feature를 추출하고 Dense layer는 추출된 feature를 입력받아 이미지를 적당한 카테고리로 분류한다.
이 때 얕은(입력층에 가까운) CONV layer일수록 단순한 특성 - 윤곽선, 음영 등 - 을 추출하고 깊은(출력층에 가까운) CONV layer일수록 복잡한 특성 - 동물 모양, 특정 색상 조합 등 - 을 추출한다.
2012년 ILSVRC에서 우승한 AlexNet이 유행시킨 구조라 할 수 있겠다. 딥러닝을 사용해서 효과적으로 이미지를 분석할 수 있다는 것을 보여준 첫 사례다.
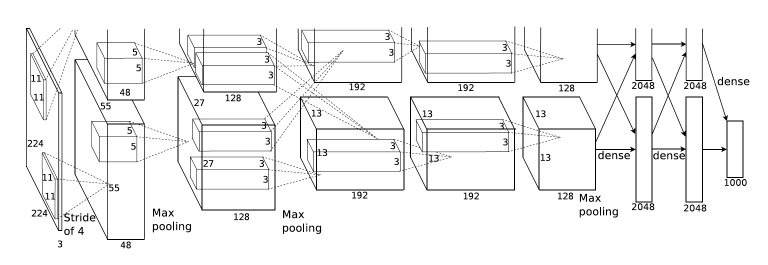
그림에서 볼 수 있듯, 5개의 CONV layer와 3개의 dense layer를 사용하여 최종적으로 1000개 카테고리에 대한 softmax 값을 출력한다. AlexNet에 대해서는 이후 기회가 될 때 자세히 다루도록 한다.
ConvNet 개선하기
1x1 convolution
어느 모형에서나 파라미터 수가 지나치게 많아지는 것은 overfitting 및 컴퓨팅 속도 저하를 의미하기에 좋지 않다. convolution 연산에 사용되는 파라미터 수(필터값 수)를 줄이기 위해서 1x1, 1xn 또는 nx1 convolution을 사용할 수 있다.
$n \times n \times 3$ 형태의 인풋 이미지에 receptive field가 3x3이 되도록, 128개의 필터를 사용해서 convolution을 한다고 가정해보자. 단순히 3x3 filter를 사용할 수도 있다. 이 경우 필요한 파라미터 수는 $3 \times 3 \times 3 \times 128 = 3456$개이다.
반면 1x1 > 1x3 > 3x1의 순서로 convolution을 한다면? 필요한 파라미터 수는 $(3 \times 1 \times 1 \times 128) + (1 \times 1 \times 3 \times 128) + (1 \times 3 \times 1 \times 128) = 384 + 384 + 384 = 1152$개 뿐이다. 같은 크기의 receptive field를 유지하면서 파라미터 수를 거의 1/3 수준으로 줄였다!
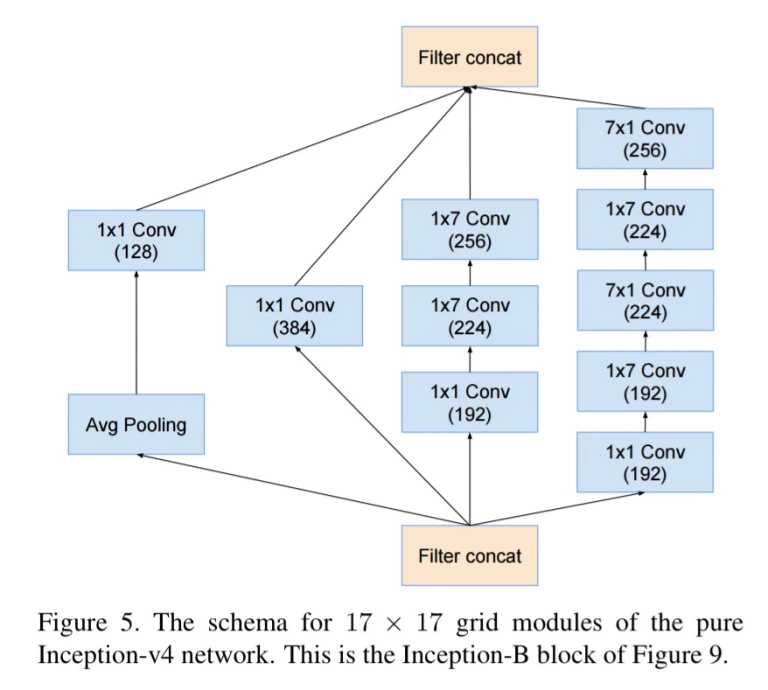
구글에서 개발한 GoogLeNet에서 바로 이 방법을 활용한 Inception 구조를 사용한다.
Dense layer를 CONV layer로 표현하기
Dense layer와 CONV layer의 차이점은 local connection 뿐이다. Dense layer에서는 이전 레이어의 모든 뉴런이 다음 레이어의 모든 뉴런과 연결되어 있는 반면(그래서 fully connected layer라고도 불린다), CONV layer에서는 이전 레이어의 일부분만이 다음 레이어의 뉴런과 연결되어 있다.
그럼 CONV layer에서 이전 레이어의 모든 뉴런을 다음 레이어와 연결시킨다면? 즉 인풋 이미지의 일부분에만 필터를 적용시키지 않고 이미지 전체에 이미지와 동일한 크기의 필터를 적용시킨다면? Dense layer와 동일한 연산을 하는 CONV layer를 만들 수 있다. 계산해보면 파라미터 수도 일치한다.
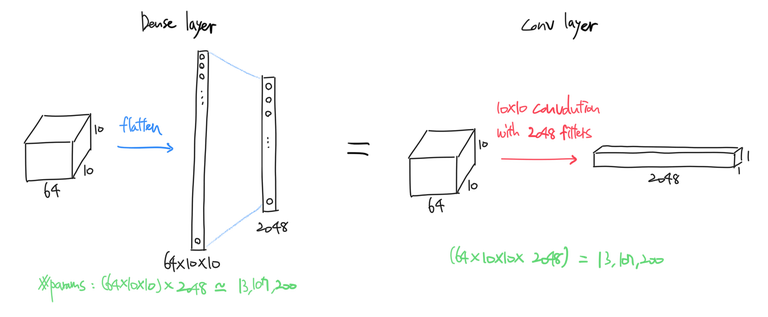
Dense layer를 CONV layer로 대체함으로써 인풋 이미지 크기를 고정하지 않아도 된다는 이익을 얻을 수 있다. 사전에 정의된 크기의 이미지를 인풋하지 않으면 오류를 뿜는 Dense layer와는 달리, CONV layer는 사전 정의된 것보다 큰 이미지를 인풋해도 오류 없이 연산을 해낸다. (다만 3차원 텐서 형태로 출력하기는 한다)
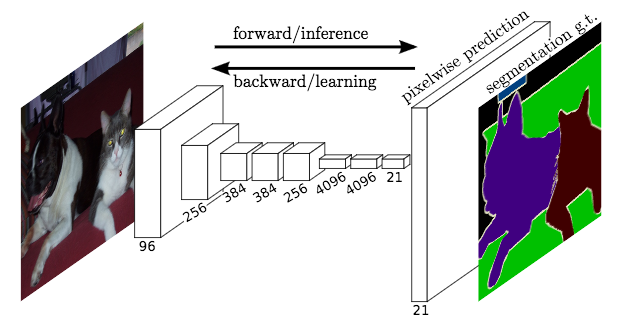
Fully Convolutional Network (FCN)이 바로 이 구조를 처음 제안한 모형이다.
특수한 Convolution
그 외에도 위에서 정의한 것과는 다른, 서로다른 문제에 특화된 특수한 convolution을 사용할 수도 있다. 예를 들어 atrous convolution은 구멍이 숭숭 뚫린 듯한 모양의 필터를 사용해서 receptive field를 더욱 향상시킨다. Deconvolution은 Convolution 연산을 역으로 수행해 추출된 feature map을 원본 이미지에 가까운 형태로 되돌린다.
특수한 convolution 연산들에 대해서는 이 페이지를 참고하면 좋다.
참고
- 이 글은 CS231n 강의록을 많이 참고했다. 원 강의록을 읽어보시기를 추천드린다.
- 1-D CONV layer는 컴퓨터 비전 분야 뿐만 아니라 앞뒤 문맥을 파악해야 하는 데이터를 분석하는 데에 쓰이기도 한다. 구글 AI 블로그의 이 글의 예시를 참고.
- 특수한 convolution 연산
- Convolution 애니메이션