인공신경망 이해하기 (2) 퍼셉트론과 신경망

•
machine learning  

$\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}$ $\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}$

이전 글에서는 분류 문제를 해결하기 위해 간단한 선형 분류기를 만드는 데에 필요한 요소들을 다루었다. 이제 우리는 분류기(모형)를 학습시키기 위해서는 판별함수 $s$, 정규화 손실항이 포함된 손실함수 $L$가 필요함을 알고 있다. 또한 학습 과정에서 최적화 과정(SGD 등)을 통해 손실이 작아지는 방향으로 가중치 $W$와 편향 $b$의 값을 반복적으로 업데이트할 수 있다.

직선(또는 hyperplane)으로 서로 다른 카테고리의 영역을 구획짓는 가장 단순한 형태의 선형 분류기를 만들어 학습시킨 결과, 붓꽃 분류 문제를 92.7%의 accuracy로 성공적으로 분류해낼 수 있었다. 그러나 직선으로 구획지을 수 없는 분류 문제에서는 매우 낮은 성능을 보였다.

이번 글에서는 직선으로 구획지을 수 없는 분류 문제를 해결하는 분류기를 다루면서 신경망 이론에 (드디어) 발을 들이고자 한다.


선형 분류기를 고집하기 (커널 트릭)

선형 분류기(linear classifier)라는 이름은 판별함수값이 가중치 $w_i$와 feature $x_i$의 선형 조합으로 표현될 수 있었기 때문에 붙은 이름이었다. 약간의 꼼수를 쓰면, 선형 분류기가 곡선적으로 판별하도록 변형시킬 수 있다.

붓꽃 분류 문제로 돌아가보자. 붓꽃 데이터에는 4차원의 feature($x_1$: 꽃받침 길이, $x_2$: 꽃받침 너비, $x_3$: 꽃잎 길이, $x_4$: 꽃잎 너비)가 존재했다. 여기에 추가로 다섯 번째 feature $x_5$를 추가해보자. 다섯 번째 feature는 꽃잎 길이의 제곱, 즉 $x_5 = (x_3)^2$이다.

이제 우리의 feature 데이터는 5차원이 되었다. 데이터의 차원이 바뀌었을 뿐, 여전히 판별함수의 식은 $s = XW + b$로 동일하다. 판별함수 식이 여전히 선형조합의 형태이므로 이 분류기 또한 여전히 선형 분류기라고 할 수 있다.

180417-1_1.png

그러나 내부를 들여다보면 이 선형 분류기는 직선적으로 카테고리를 구획짓지는 않는다.

첫 번째 관찰의 첫 번째 카테고리의 판별함수값을 보면 $s_{i1} = \sum_{j} w_{ji} x_{ij} + b_i = w_{1i} x_{i1} + w_{2i} x_{i2} + w_{3i} x_{i3} + w_{4i} x_{i4} + w_{5i} x_{i5} + b_i$이고 $x_5 = (x_3)^2$이므로, 판별함수는 다음과 같은 이차식(즉, 곡선 또는 곡면)의 형태를 띄게 된다.

\[s_{i1} = w_{5i} (x_{i3})^2 + w_{1i} x_{i1} + w_{2i} x_{i2} + w_{3i} x_{i3} + w_{4i} x_{i4} + b_i\]

단순히 판별함수에 학습시키는 인풋 데이터를 변형함으로써 곡선적으로 분류하는 선형 분류기를 만들 수 있는 것이다. 인풋 데이터를 일정 규칙에 따라 변형시켜주는 함수를 커널 함수(kernel function)라고 하며 커널 함수를 사용해서 곡선적으로 분류하는 선형분류기를 만드는 것을 ‘커널 트릭(kernel trick)을 사용한다’고 한다.


XOR 문제

‘exclusive OR (XOR)’라고 불리는 다음과 같은 문제가 있다. 이런 형태의 데이터는 하나의 함수만으로는 분류가 불가능하다.

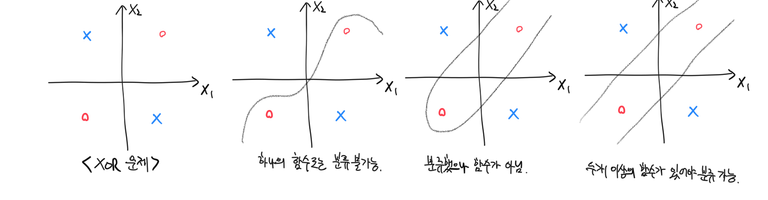
xor_problem.png

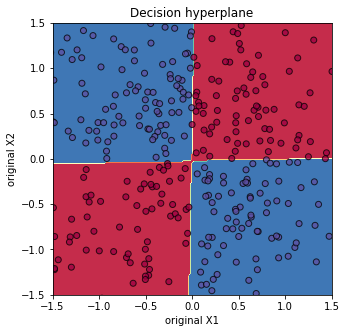
하지만 다항(polynomial) 커널을 사용해서 feature를 변형하면 직선적으로 분류가 가능해진다. 다항 커널을 사용해서 변형한 feature 값에 softmax 선형 분류기를 구현한 다음, 변형하기 이전 원래 feature 값에 판별 hyperplane을 나타내보면 아래처럼 곡선적으로 분류가 되었음을 확인할 수 있다.

softmax+polynomial_kernel.png


선형 분류기를 넘어서

똑같은 선형 분류기를 사용해도 단순히 인풋 데이터를 변형하기만 해도 몇몇 형태의 곡선적 데이터는 성공적으로 분류할 수 있다. 그러나 커널 트릭은 근본적인 해결책은 되지 못한다. 분류기의 형태는 여전히 단순 선형조합만으로 표현되므로, 커널 트릭으로 해결할 수 있는 곡선적 분류 문제는 극히 일부이다. 따라서 우리는 모든 경우에도 높은 성능을 내는 비선형 분류기(non-linear classifier)를 구현할 필요가 있다.

어떤 형태의 곡선적 또는 비선형 문제든지 모두 학습이 가능하도록 고안된 분류 모형이 인공신경망(Artifical Neural Network; ANN)이다.


퍼셉트론

인공신경망에 다이빙하기 전에 퍼셉트론의 개념을 다룰 필요가 있다. 퍼셉트론(perceptron; 또는 그냥 neuron이라고도 함)은 시신경세포를 수학적으로 비유/모델링하는 과정에서 탄생한 분류기이다. 실제 시신경세포의 작용과는 (당연히) 큰 차이가 있다. 입력 정보의 강도에 따라 출력 여부가 결정된다는 점(즉, 출력이 thresholding된다는 점)에 착안해서 만들어진 분류기라고 이해하면 좋다.

perceptron.png

퍼셉트론 하나의 판별함수는 다음과 같이 식으로 나타낼 수 있다.

\[s = f(XW + b)\]

가중치 $W$와 feature $X$의 선형조합 $XW + b$에 함수 $f$를 씌운 형태이다. 여기서 함수 $f$는 출력의 여부 및 세기를 결정(뉴런으로 비유하자면 활성화 여부와 정도를 결정)한다고 해서 활성화 함수(activation function)라고 부른다. 활성화 함수로는 항상 비선형 함수를 사용한다.

활성화 함수를 softmax 함수로 설정하고 손실함수를 cross-category loss($L_i = - \sum_{j} p_{y_i} log{p_j}$)로 설정한 퍼셉트론은 앞서 구현한 softmax 분류기와 동일한 분류기가 된다. 비슷한 방법으로 손실함수를 max-margin loss로 설정하면 퍼셉트론은 서포트 벡터 머신이 된다. 결국 퍼셉트론은 선형 분류기에 약간의 비선형 트윅(활성화 함수)을 가한, 선형 분류기의 연장이다.

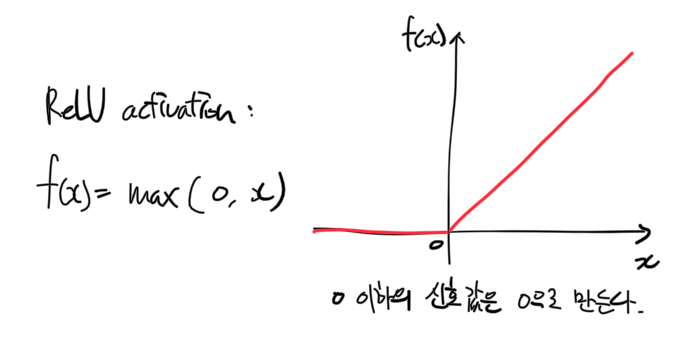
로지스틱 함수 외에도 쌍곡탄젠트 함수 등 몇 가지 활성화 함수가 제시되어 있지만 일반적으로 가장 많이 사용하는건 ReLU(Rectified Linear Unit)라는 녀석이다. ReLU activation을 식으로 나타내면 다음과 같고, 이는 0 이상 강도의 신호만을 출력하게 하는 0-역치값(zero-threshold) 역할을 한다.

ReLU.png


다중층 퍼셉트론: 신경망

다시 XOR 문제로 돌아가보자. 지금까지의 내용을 정리해보면 이렇다.

  1. XOR 문제는 하나의 판별함수로는 분류할 수 없는 문제다 (두 개 이상의 함수가 필요하다).
  2. 퍼셉트론은 시신경세포에 대한 매우 단순한 수학적 모형이다.
  3. 퍼셉트론은 선형 분류기에 비선형 변형을 가한 출력값을 반환한다 (비선형 함수값을 준다).

이 내용을 보고 이렇게 생각해볼 수 있다:

  1. 그럼 함수 두 개 이상을 만들면 되겠네.
  2. 신경뭉치(더 나아가서, 뇌)처럼 퍼셉트론을 여러개 연결시키면 어떨까?
  3. 퍼셉트론은 곧 비선형 함수 한 개니까, 퍼셉트론 뭉치는 두 개 이상의 함수의 조합이다.
  4. 그럼 퍼셉트론 뭉치로 XOR를 포함한 비선형 분류 문제를 해결할 수 있겠다!

이렇게 해서 퍼셉트론을 여러 층 쌓아 하나의 거대한 비선형 분류기를 만들 수 있다. 이를 다중층 퍼셉트론(multi-layer perceptron; MLP) 또는 신경망(Neural Network; NeuralNet; NN)이라고 부른다.

신경망은 다음과 같은 구성으로 이루어져 있다.

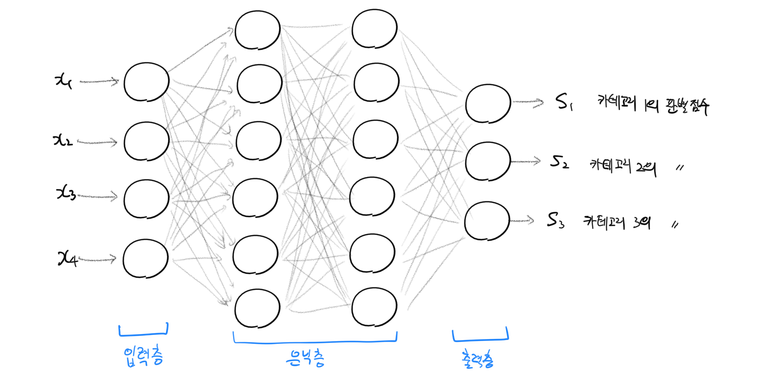
neural_network.png

  • 입력층(input layer): 학습 데이터 feature를 입력받는 층이다. Feature의 차원 수(붓꽃 데이터의 경우 4)만큼의 뉴런 갯수를 가진다. 입력 층은 MLP 당 하나 뿐이다.
  • 은닉층(hidden layer): 입력층과 출력층 사이의 모든 층을 뜻한다. 입력층에서 입력받은 raw data에 대해 다수의 비선형 판별함수가 학습되는 층이다. 그림의 신경망에는 각각 6개 뉴런을 가지는 2개의 은닉층이 있다.
  • 출력층(output layer): 데이터에 대해 각 카테고리에 대응하는 판별함수값을 출력하는 층이다. 카테고리 수(붓꽃 데이터의 경우 3)만큼의 뉴런 갯수를 가진다. 출력층도 입력층과 같이 MLP 당 하나 뿐이다. 출력층에 있는 뉴런은 활성화함수를 가지지 않는 경우가 일반적이다.
  • 신경망은 “n-층 신경망”과 같이 층 갯수로 이름을 붙인다. 이 때 입력층은 갯수를 셀 때 포함하지 않는다. 그림의 신경망은 3층 신경망이다.
  • 같은 층에 있는 뉴런끼리는 연결되어 있지 않다.
  • 한 층에 있는 뉴런은 다음 층에 있는 모든 뉴런과 연결된다 (“fully-connected layer”).
  • 뉴런의 출력은 한 방향(출력층 -> 은닉층1 -> 은닉층2 -> … -> 출력층)으로만 전파된다.

은닉층이 하나 있는 2-layer neural net은 식으로 다음과 같이 표현할 수 있다.

\[s = hW_2 + b_2 = f(XW_1 + b_1)W_2 + b_2\]

일반적인 n-layer neural net도 다음과 같이 표현 가능하다.

\[s = h_{n-1}W_n + b_n = f_{n-1}(h_{n-2}W_{n-1} + b_{n-1})W_n + b_n = \cdots\]

활성화함수의 중요성이 여기서 드러난다. 비선형 활성화함수가 매 층 사이에 존재하지 않는다면 위의 식은 결국 가중치와 feature의 선형조합으로 정리된다. 다시 말해 활성화함수가 없다면 신경망은 선형 분류기와 동일해진다. 활성화함수가 신경망 분류모형에 비선형성(non-linearity)를 제공한다고 이해할 수 있는 대목이다. 이론적으로 하나 이상의 은닉층을 갖는 신경망으로 존재하는 모든 비선형 함수를 근사할 수 있음이 증명되어 있다.

Feature 데이터는 입력층 -> 은닉층 -> 출력층의 순서로 전파되어 판별함수값 $s$로 변환되며, 이 과정을 일컬어 ‘feed-forward‘라고 한다.


신경망 학습시키기

신경망을 학습시키는 데에도 선형 분류기를 학습시킬 때와 마찬가지로 손실함수값 $L$를 계산하고, 손실함수값 $L$의 가중치 $W$에 대한 그라디언트를 계산해야한다. 계산한 그라디언트의 반대 방향으로 반복적으로 가중치를 업데이트하면 우수한 성능을 내는 신경망 분류기를 얻을 수 있을 것이다.

그런데 신경망에서의 그라디언트 계산은 선형 분류기에 비해 복잡하다. 한 차례 편미분으로 쉽게 그라디언트를 구할 수 있었던 선형 분류기에서와 달리, 신경망의 손실함수는 가중치 $W$로 직접 편미분하기에는 식이 복잡하다.

그래서 신경망의 그라디언트는 미분의 연쇄법칙(chain rule)을 사용해서 단계적으로 계산한다.


선형 분류기의 예시

비교적 단순한 예시부터 살펴보자.

앞서 구현한 선형 Softmax 분류기는 은닉층이 없는 신경망이라고 생각할 수 있다. 손실함수로 softmax 손실 + Ridge 정규화 손실($L = \sum_i L_i + \alpha R(W)$, $L_i = - \log{\frac{e^{f_{y_i}}}{\sum_j e^{f_j}}}$, $R(W) = \sum_i \sum_j w_{ij}^2 + \sum_k b_k^2$)을 둔다고 할 때, 이 선형 분류기의 feed-forward는 아래와 같이 왼쪽(입력측)에서 오른쪽(출력층) 방향으로 일어난다.

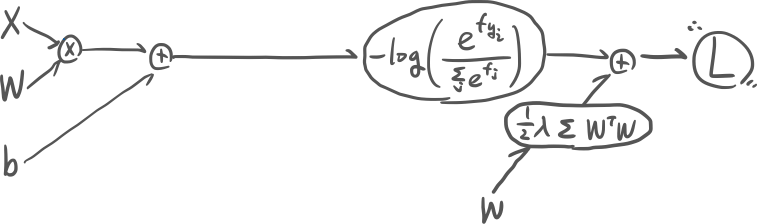
backprop_1.png

그라디언트의 계산은 feed-forward의 반대 방향으로 일어난다: 출력층에서 입력층의 방향으로 단계적으로 계산된다.

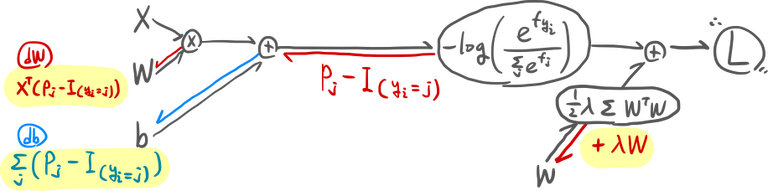
backprop_2.png

즉 연쇄법칙에 의해 $\frac{\partial L}{\partial W} = \frac{1}{N} \sum_i \frac{\partial L_i}{\partial W} + \frac{\partial R(W)}{\partial W} = \frac{1}{N} \sum_i \frac{\partial L_i}{\partial f} \frac{\partial f}{\partial W} + \frac{\partial R(W)}{\partial W}$로 그라디언트를 계산할 수 있다.


2-layer Neural Net의 예시

신경망에서도 똑같은 방법으로 역전파할 수 있다. 그림은 좀 더 복잡하다.

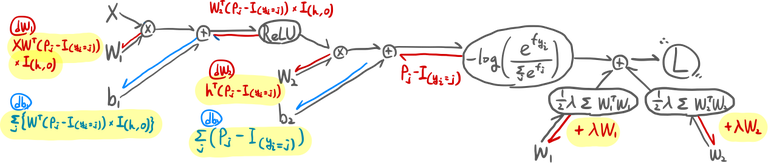
backprop_3.png

이처럼 연쇄법칙을 사용해서 단계적으로, 출력층에서 입력층 방향으로 그라디언트 값을 전파하는 계산법을 역전파(back-propagation; backprop)이라고 한다.


2-layer Neural Net 구현

붓꽃 분류 문제

판별함수(신경망 구조)와 손실함수도 정의했고 그라디언트 계산법도 알았으니 이제 직접 붓꽃 종을 분류하는 신경망을 구현해볼 시간이다. 선형 분류기를 구현했을 때와 마찬가지로 붓꽃 측정치 중에서 2개의 차원(꽃받침 길이, 꽃잎 길이)만을 사용했다.

  • 데이터 손실로 softmax loss를 가지고
  • 정규화 손실로 Ridge 정규화항을 가지며,
  • 2개 뉴런이 있는 입력층 하나와
  • 100개 뉴런이 있는 은닉층 하나와
  • 3개 뉴런이 있는 출력층을 가지는,
  • back-propagation으로 그라디언트를 계산하여 가중치를 업데이트하는

2층 신경망을 구현한 코드는 아래와 같다.

def train_nn(x, y, D, K, reg=.001, eta=.05, epochs=5000):
    # initialize weights
    W1 = np.random.randn(D, 100) * 0.01
    b1 = np.zeros((1, 100))
    W2 = np.random.randn(100, K) * 0.01
    b2 = np.zeros((1, K))

    # training process
    losses = []

    for epoch in range(epochs):
        h = np.maximum(0, x.dot(W1) + b1) # hidden layer
        f = h.dot(W2) + b2 # final layer

        # backprop to hidden layer
        p = np.exp(f) / np.sum(np.exp(f), axis=1, keepdims=True)
        dhidden = p.copy()
        dhidden[range(x.shape[0]), y] -= 1
        dhidden /= x.shape[0]
        dW2 = (h.T).dot(dhidden) + reg * W2
        db2 = np.sum(dhidden, axis=0, keepdims=True)

        # backprop the activation (relu)
        drelu = (dhidden).dot(W2.T)
        drelu[h <= 0] = 0

        # backprop to input layer
        dW1 = (x.T).dot(drelu) + reg * W1
        db1 = np.sum(drelu, axis=0, keepdims=True)

        # update weights
        W1 -= eta * dW1; b1 -= eta * db1
        W2 -= eta * dW2; b2 -= eta * db2

        # compute loss
        data_loss = -np.sum(np.log(p[range(x.shape[0]), y])) / x.shape[0]
        reg_loss = 0.5 * reg * (np.sum(W2**2) + np.sum(W1**2))
        loss = data_loss + reg_loss
        losses.append(loss)
        if epoch % 1000 == 0:
            print("{}: loss={}".format(epoch, loss))
 
    return W1, b1, W2, b2, losses

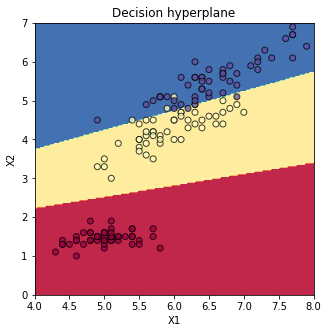
2-layer-neural-net.png

학습시킨 신경망으로 붓꽃 종을 분류한 결과 96%의 accuracy를 얻을 수 있었다 (선형 분류기에서는 92.7%였다).

자동으로 그라디언트를 계산해주는 Tensorflow등의 프레임워크를 사용하면 더 간단히 구현할 수 있다. 거기에 Keras와 같은 high-level 프레임워크를 사용하면 훨씬 더 간단히 구현할 수 있다. 그냥 구현은 남에게 맡기고 간단히 체험만 해보고싶다면 구글에서 제공하는 웹페이지에서 클릭 몇 번으로 간단한 신경망을 학습시킬 수 있다.


비선형 데이터 분류 문제

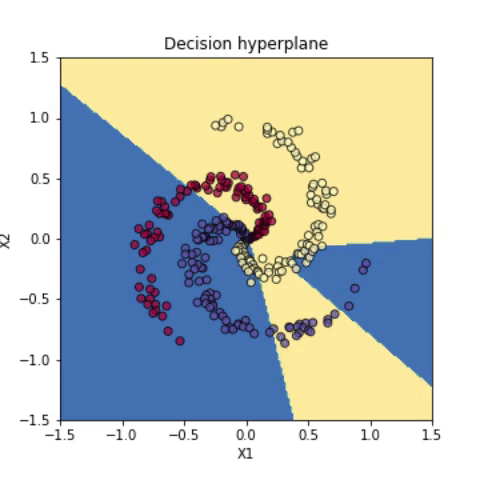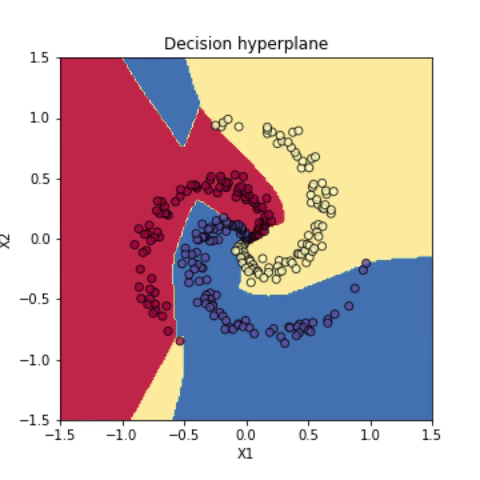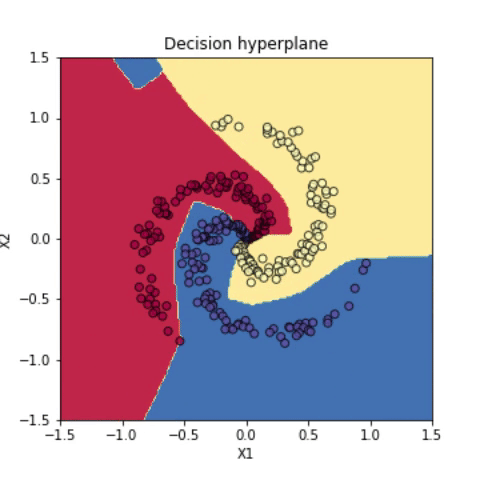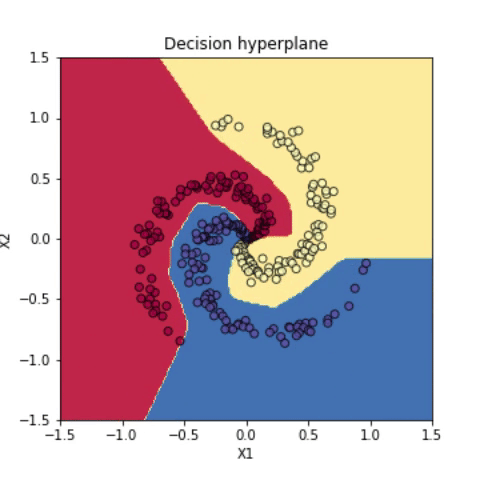
붓꽃 분류 문제는 선형 분류기로도 쉽게 해결할 수 있었다. 신경망은 비선형 분류 문제에서 더욱 빛난다. 선형 분류기를 사용했을 때는 엉망진창으로 분류되던 데이터가 신경망을 사용한 분류에서는 매우 높은 accuracy (~99%)로 해결되는 것을 확인할 수 있다.

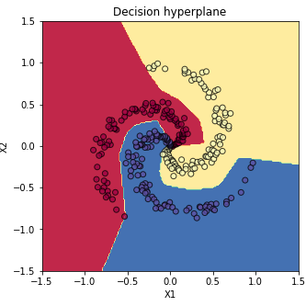
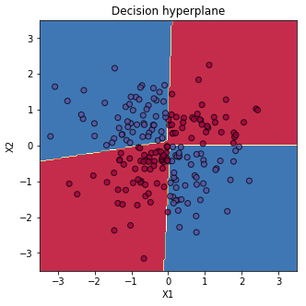
2-layer-neural-net2.png 2-layer-neural-net3.png

지금까지 가장 단순한 신경망 구조인 MLP를 이용해서 비선형 분류 문제를 해결해 보았다. 다음 글에서는 신경망 구조를 학습시킬 때 주의깊게 살펴야 하는 점들에 대해 다루어보겠다.


참고

  • 이 글은 CS231n 강의록을 많이 참고했다. 원 강의록을 읽어보시기를 추천드린다.
  • polynomial kernel을 사용한 softmax classifier 및 2-layer neural net를 구현한 전체 코드는 이 노트북에서 확인할 수 있다.
  • 애니메이션을 만들어보면 decision hyperplane이 학습되고 있는 상황을 확인할 수 있다. 꽤 재미지고 신기하다.

2-layer-neural-net4.png