인공신경망 이해하기 (1) 선형 분류기
인공지능이 알파고의 형태로 대중에 모습을 드러내 굉장한 충격을 가져다 준 이후, 인공지능에 대한 관심은 그야말로 폭발했다. 조류 인플루엔자, 어도비 일러스트레이터의 약자로 더 자주 쓰였던 AI는 대부분의 경우 인공지능을 뜻하게 되었다.
그러나 단순한 신경망 구조는 생각보다는 어렵지 않은 개념임에도 인공지능이라는 단어에서 오는 중압감과 다소 투박하게 표현된 수식 때문인지, 엔지니어 분야 밖의 대중적인 개념이 되는 데에는 실패한 듯하다.
여기서는 인공지능에 접점이 없었던 사람을 대상으로 현대 인공지능의 시작과 끝이라 할 수 있는 인공신경망(artificial neural network; ANN)의 개념을 여러 글에 거쳐 풀이해보고자 한다. 작성자 본인도 부족한 학생인지라 되도록 직관으로 이해가능하게 작성하려고 노력했다.
들어가기 전에
쉽게 설명하겠다는 명목 하에 개념 설명에 필수적인 내용을 빼먹는 건 설명의 본분을 다하지 않는거라 생각한다. (슬프게도?) 주제가 주제이다보니 제대로 이해하기 위해서는 수학과 컴퓨팅에 대한 기초가 필요하긴 하다.
행렬 연산, 미분에 대한 기초가 있으면 이해에는 큰 어려움이 없을 거라 생각한다. 덧붙여 기하적 해석이 가능하면 더욱 좋다. 또, 어떤 것이든 사용하는 데에 불편함이 없는 프로그래밍 언어가 하나 있으면 좋다. 여기서는 코드가 필요한 경우 Python 2.7.x 문법과 패키지를 사용했다.
해결하고자 하는 문제
여기서 신경망으로 풀어보려 하는 문제는 분류(classification)다. 분류 문제는 이전의 관찰 데이터를 바탕으로 새로운 관찰이 어떤 카테고리에 속하는지를 예측하는 문제다. 이 때 이전의 관찰 데이터에는 각각의 관찰이 어떤 카테고리에 속한 것이었는지에 대한 정보(라벨)가 함께 제공되어야 한다.
- 스팸 메일 예측이 분류 문제의 대표적인 예시다. 지금까지 받은 모든 메일들(이전의 관찰 데이터)을 바탕으로 새로 온 메일(새로운 관찰)이 스팸인지 아닌지를 분류하는 것이다. 이 때, 지금까지 받은 메일들이 스팸인지 아닌지(‘라벨’이라 한다)는 알고있어야 한다(라벨 정보가 있어야함).
- 동식물의 종을 맞추는 문제도 분류 문제의 일종이다. 붓꽃과에 속하는 3개 식물종의 꽃잎 너비와 길이, 꽃받침 너비와 길이에 대한 측정치(이전의 관찰 데이터)를 바탕으로 새로 관찰한 붓꽃과 식물(새로운 관찰)이 3개종 중 어느 종일지를 추측할 수 있다. 역시나 각각의 측정치(‘특징’ 또는 ‘feature‘라 부른다)가 어떤 식물종의 개체로부터 측정된 것인지에 대한 정보(‘라벨‘)는 알고 있어야 한다.
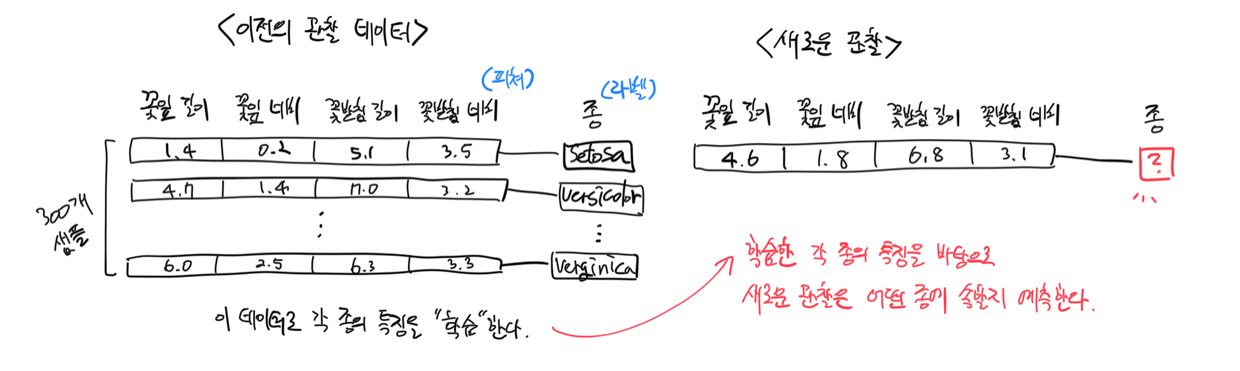
아주 단순화한 분류 문제의 해결 흐름은 다음과 같다.
- 이전의 관찰 데이터를 준비한다.
- 이전 데이터를 바탕으로 각 카테고리에 속한 관찰들의 특징을 알고리즘이 ‘학습한다’.
- 알고리즘이 학습한 내용을 바탕으로 새로운 관찰이 어떤 카테고리에 속할지 예측한다.
위에서 언급한 붓꽃과 식물의 측정 문제를 통해서 기계학습의 기초와 신경망 이론을 다룰 것이다. 이제 관찰 데이터는 준비가 됐고, 올바르게 종을 분류하는 분류기를 만들 시간이다.
가장 단순한 분류법 - 직선적 분류
꽃잎, 꽃받침 길이와 너비라는 수치 데이터를 보고 종을 분류하는 문제에서, 가장 먼저 단순하게 생각해 볼 수 있는 분류기는 직선적으로 데이터를 구획해주는 놈이다.
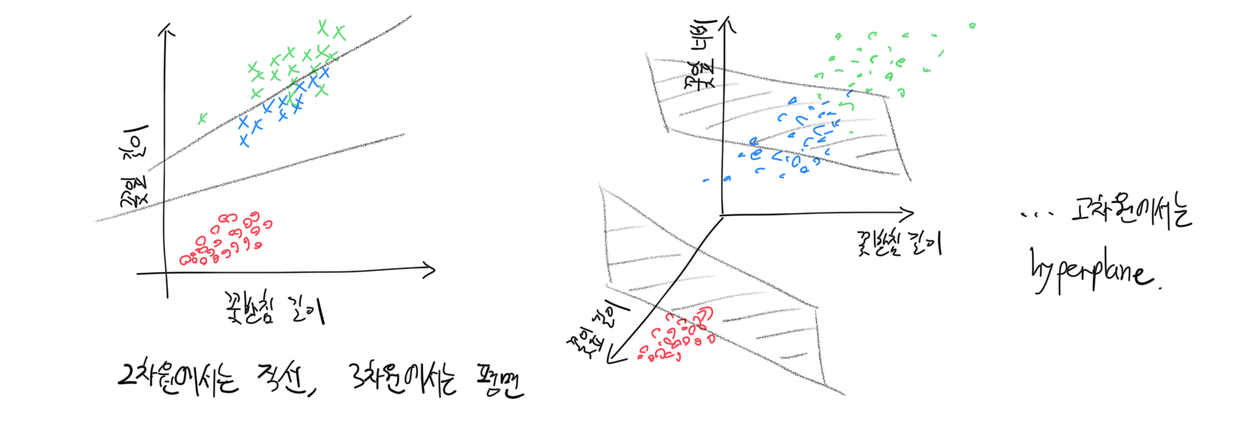
즉, 직선(데이터가 3차원인 경우는 평면, 4차원 이상의 데이터에서는 hyperplane)을 그어 서로 다른 라벨을 지닌 데이터를 분리해주는 것이다.
데이터를 구획해주는 이 직선(또는 평면, 또는 hyperplane)의 함수를 우리는 판별 함수 (decision function)라 부른다. 각 관찰에 대한 판별함수값은 판별 점수(decision score), 또는 클래스 점수(class score; 관찰이 해당 클래스=카테고리에 속할 가능성)라고 부르기도 한다.
선형 판별함수는 우리가 익히 알고 있는 다음과 같은 꼴의 식으로 표현할 수 있다.
\(s = wx + b\) (2차원 데이터에서, 직선 판별함수의 경우)
\(s = w_1x_1 + w_2x_2 + b\) (3차원 데이터에서, 평면 판별함수의 경우)
여기서 $s$는 관찰 값에 대한 판별 점수, $x$는 관찰의 features 데이터, $w, b$는 각각 판별함수의 ‘기울기’와 ‘절편’이다.
이 판별함수를 고차원에 대해 일반화해서 다음과 같이 행렬식으로 간단히 표현할 수 있다.
\[s = XW + b\]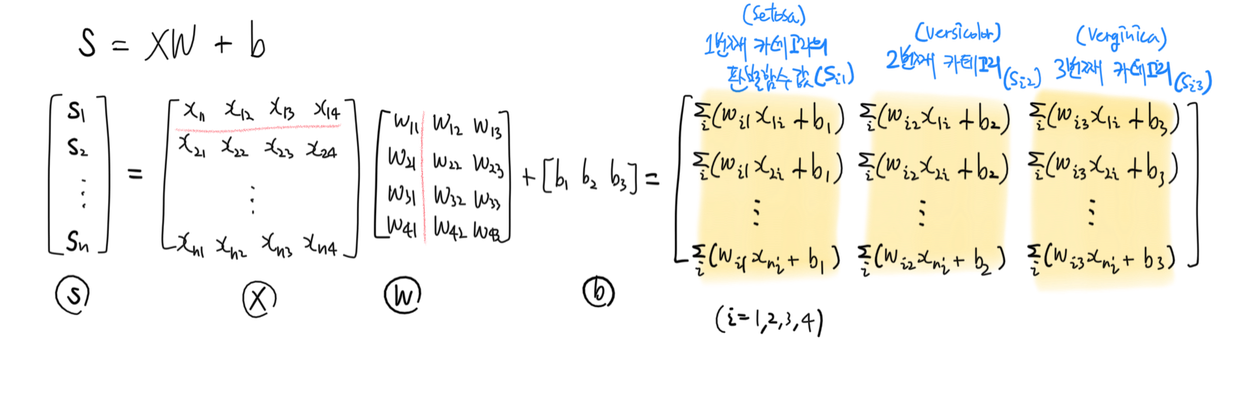
여기서 $s$는 관찰 값에 대한 판별 점수의 행렬, $X$는 관찰한 features의 행렬, $W, b$는 각각 판별함수의 ‘기울기’(?) 행렬과 ‘절편’(?) 벡터이다.
직선의 경우 ‘기울기’와 ‘절편’이라 표현하는 것이 직관적이나, hyperplane에서는 이 표현이 직관적이지 않으므로 이제부터는 $W$를 ‘가중치 (weight)’ 행렬, $b$를 ‘편향 (bias)’ 벡터라 부르기로 한다.
위의 판별함수는 데이터의 차원만 다를 뿐, 모두 가중치 $w_i$와 feature $x_i$의 선형조합의 꼴로 표현할수 있으므로 선형 판별함수라 할 수 있다.
자, 이제 우리는 다음과 같이 선형 분류기의 뼈대를 만들었다.
\[s = XW + b\]이제는 이 분류기가 붓꽃 종을 올바르게 예측할 수 있도록 각 붓꽃 종의 특징을 판별함수에 ‘학습시킬’ 차례다.
가중치와 편향을 이해하기
가중치 $w_i$는 “i번째 feature가 라벨의 예측에 끼치는 영향”이라고 해석할 수 있다. i번째 가중치값 $w_i$의 값의 절대값이 클 수록 i번째 feature가 예측에 미치는 영향이 크다고 할 수 있고, 따라서 i번째 feature가 라벨의 예측에 중요한 정보라고 판단할 수 있다. 또한 가중치값의 부호에 따라 예측에 미치는 영향이 양의 영향인지, 음의 영향인지 알 수 있다.
편향 $b_i$에 대한 해석은 가중치에 비해서는 덜 명확하다. 편향 $b_i$ 값은 i번째 feature $x_i$의 값이 0일 때 예측되는 라벨의 값으로 이해할 수 있다. 분류기 식에서 편향을 제거한다면 (즉 위의 붓꽃 예시에서 $b_i = 0, i = 1,2,3,4$ 이면) 판별함수는 항상 원점을 지나는 형태일 것이다. 따라서 편향은 기하적으로는 판별함수가 원점을 지나지 않아도 되도록 해주는 역할을 한다고 이해할 수 있다.
우리가 세운 선형 분류기 식에서, $X$는 관측된 데이터이므로 마음대로 바꿀 수 있는 값이 아니다. 대신분류기가 데이터 $x_i$를 보고 학습함에 따라 새로운 관찰을 더 정확히 분류할 수 있는 방향으로 가중치 $w_i$와 편향 $b_i$의 값이 변하게 된다. 기하적으로는 더 정확히 판별 직선(혹은 평면, 또는 hyperplane)을 긋는 방향으로 기울기와 절편 값이 변한다고 이해할 수 있다.
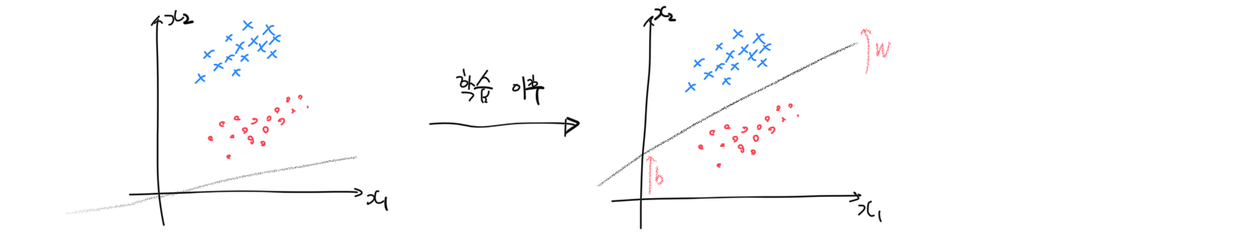
그렇다면 어떻게 해야 더 분류를 잘 하는 방향으로 가중치와 편향 값을 변화시킬 수 있을까? 어떻게 해야 선형 분류기를 학습시킬 수 있을까?
손실 함수 (loss function)
선형 분류기가 학습을 하고 있는지, 즉 더 나은 방향으로 선형 분류기의 가중치와 편향 값이 변하고 있는지를 판단하기 위해서는 분류기의 성능을 평가하는 손실 함수(loss function)를 설정해야 한다.
손실 함수는 분류기의 성능이 낮을수록 손실 함수 값이 커지는 특성을 가져야 한다 (분류기의 성능이 높을수록 손실 함수 값이 작아져야 한다). 결국 손실 함수의 값이 크다는 것은 분류기가 카테고리를 잘 예측하지 못하고 있다는 것을 의미한다 - 그래서 이름이 ‘손실 함수’다!
손실 함수를 어떻게 설정하느냐에 따라 선형 분류기의 특성이 달라진다.
판별함수값을 “확률”이라고 생각하기
각 샘플의 판별함수값을 해당 카테고리에 속할 ‘확률’이라고 해석할 수 있다. 이 때 샘플이 k번째 카테고리에 속했을 확률 $p_k$는 다음과 같다.
\[p_k = \frac{e^{s_k}}{\sum_{j} e^{s_j}}\]여기서 $s_k$는 해당 샘플의 k번째 카테고리에 대응하는 판별함수값이다. $p_k$는 [0, 1] 사이의 값을 가지므로 일종의 ‘확률’ 또는 ‘확신의 정도’라고 해석할 수 있다.
계속해서 i번째 샘플의 손실 $L_i$은 다음과 같이 설정할 수 있다.
\[L_i = - \log{e^{s_{y_i}} \over {\sum_{j} e^{s_j}}} = - \log{p_{y_i}}\]여기서 $s_{y_i}$는 i번째 샘플의 진짜 라벨(실제 속해있는 카테고리)의 판별함수값, $s_j$는 j번째 카테고리의 판별함수값이다. 따라서 i번째 샘플의 손실 $L_i$는 카테고리를 올바르게 예측했을 확률의 로그값에 음수를 취한 것이다.
최종적으로 전체 샘플 $N$개의 손실 $L$은 각 샘플의 손실의 평균치로 계산한다.
\[L = \frac{1}{N} \sum_{i} {L_i} = - \frac{1}{N} \sum_{i} \log{e^{s_{y_i}} \over {\sum_{j} e^{s_j}}} = - \frac{1}{N} \sum_{i} \log{p_{y_i}}\]손실함수 $L$의 값은 따라서 카테고리를 올바르게 예측했을 확률의 로그값의 평균에 음수를 취한 것이라 해석할 수 있다. 이 값은 분류기가 샘플들의 카테고리를 잘 예측할 때 작아지고 예측 성능이 나쁠수록 커진다.
여기서 $f(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}$ 꼴의 함수는 $x_i$들 중에서 가장 큰 값을 찾아주는 $\max$ 함수를 미분가능한 함수로 근사한 것이기에 softmax 함수라고 부른다. Softmax 함수 꼴이 사용되는 이 손실함수는 softmax 손실함수라 칭한다. Softmax 손실함수를 사용하는 선형 분류기는 Softmax 분류기(‘다중 클래스 로지스틱 회귀’라고도 함)가 된다.
당연히, softmax 손실함수 외에도 수많은 손실함수가 존재한다. 일례로 max-margin 손실함수를 사용하는 선형 분류기는 서포트 벡터 머신(support vector machine; SVM)이 된다.
다른 손실함수는 차차 다루기로 하고 여기서는 softmax 손실을 사용하기로 한다.
정규화 손실 추가하기
feature:label 데이터쌍만으로 손실함수를 만들면 학습시킨 데이터에서만 높은 성능을 내도록 분류기가 필요 이상의 학습을 하게 될 수도 있다. 학습 데이터에서 실제 카테고리 예측과는 상관이 없는 노이즈까지 학습하는 이 현상을 과적화(overfitting)라 한다.

따라서 오버피팅이 발생하지 않도록 손실함수에 제약을 줘야한다. 되도록 단순한 형태의 판별함수가 되도록 손실함수에 제약을 주는 것을 정규화한다(regularize)고 한다.
가장 단순한 정규화는 가중치의 제곱합이 커질수록 손실함수가 커지도록 다음의 정규화 손실 $R(w)$ 항을 손실함수에 추가하는 것이다.
\[R(w) = \sum_{i} \sum_{j} w_{ij}^2 + \sum_{k} b_k^2\]여기서 $w_{ij}$는 가중치 행렬 $W$의 i행 j열 성분, $b_k$는 편향 벡터 $b$의 k번째 성분이다. 이 방식을 Ridge 정규화 (또는 L2 정규화)라고 하며 전체적으로 고르고 작은 값의 가중치로 이루어진 가중치 행렬을 선호하는 방향으로 분류기를 정규화한다.
Ridge 최적화를 적용한 최종 손실함수는 다음과 같이 표현된다.
\[L = \frac{1}{N} \sum_{i} L_i + \lambda R(w)\]여기서 $\lambda$는 0 이상의 값으로 정규화 강도 (regularization strength)라고 하며 정규화 손실과 데이터 손실 사이의 균형을 맞추는 역할을 한다. $\lambda$ 값이 클수록 정규화의 강도가 강해진다.
Ridge 외에도 Lasso, Elastic Net 등 다양한 정규화 방법이 있다. 이에 대해서는 추후에 살펴보기로 한다.
손실함수를 설정한 후엔 선형 분류기를 학습시키면 된다.
수치적 최적화 - 경사 하강법
‘분류기를 학습시킨다’는 것은 손실함수값을 작게 만드는 가중치, 편향값을 찾는 것을 의미한다. 이상적인 가중치, 편향의 값은 손실함수를 최소로 하는 값($\arg\max_{w} L$)이다. 곧 ‘분류기를 학습시킨다’는 것은 ‘손실함수에 대한 $W, b$의 최적화 문제’이다.
많은 경우 손실함수를 분석적으로 최적화하는 것은 어렵다. 손실함수에 미분불가능한 구간이 존재하거나 분석적으로 해를 구하기 복잡할 수 있기 때문이다 (아예 전역해가 존재하지 않을 수도 있다). 대신 수치적으로 손실함수를 최적화할 수 있다.
수치적 최적화의 가장 단순한 형태는 경사 하강법(gradient descent optimization)이다. 손실함수 $L$을 $W$과 $b$에 대해 편미분하여 경사(gradient; 증가율과 같은 개념) $\frac{\partial L}{\partial W}$과 $\frac{\partial L}{\partial b}$를 계산한 다음, 경사의 반대 방향으로 가중치를 “굴러 떨어뜨리는” 것이다.

편의상 그림에서는 볼록함수의 예시를 보였지만 미분불가능한 구간이 있는 함수도 이 방법으로 최적화할 수 있다.
가중치를 “굴러 떨어뜨려서” 새로운 값으로 업데이트하는 과정을 식으로 표현하면 다음과 같다.
\[W_{new} = W_{old} - \eta \frac{\partial L}{\partial W} \\ b_{new} = b_{old} - \eta \frac{\partial L}{\partial b}\]여기서 $\eta$는 학습률(learning rate)라고 부르고 가중치 값을 얼마나 크게 이동할 것인지를 결정하는 역할을 한다. 손실함수가 로컬 최솟값으로 수렴할 때까지 가중치 업데이트를 반복하면 수치적 최적화를 수행할 수 있다.
실제로 가중치 업데이트를 할 때는 제한된 메모리를 이유로 위와 같이 전체 가중치 값 전체 $W$를 사용하는 대신 이 중 일부만을 무작위로 선택해서 경사를 계산, 업데이트 하는 경우가 대부분이다. 매 업데이트 시에 가중치 중 하나 $W_{ij}$만을 선택해서 경사를 계산하는 경우, 다음과 같이 식으로 표현할 수 있다.
\[W_{new} = W_{old} - \eta \frac{\partial L}{\partial W_{ij}} \\ b_{new} = b_{old} - \eta \frac{\partial L}{\partial b_{k}}\]이 방법을 확률적 경사하강법 (Stochastic gradient descent; SGD)이라 한다. 이 경우 경사의 정확도는 일반 경사하강법보다 떨어지지만 훨씬 적은 메모리로 빠르게 경사를 계산해낼 수 있고, 실시간으로 새로이 추가된 관찰값을 이용하여 가중치를 업데이트할 수 있다는 장점이 있다.
이 외에도 단순 경사 하강법보다 훨씬 좋은 수치적 최적화 방법들이 다수 있으나 추후에 다루기로 한다. 붓꽃 데이터의 예시에서는 메모리가 크게 필요치 않으므로 둘 중 어떤 방법을 선택하든 문제없다.
여기까지 선형 분류기를 만들고 학습시키는 데에 필요한 최소한의 내용을 다루었다. 이제는 직접 분류기를 구현해보자.
선형 분류기 구현
- 선형 판별함수($s = XW + b$)를 사용하고,
- Softmax 손실함수($L_i = - \frac{1}{N} \sum_{i} \log{e^{s_{y_i}} \over {\sum_{j} e^{s_j}}}$) 및
- Ridge 최적화($R(w) = \sum_{i} \sum_{j} w_{ij}^2 + \sum_{k} b_k^2$)를 적용하여 손실함수를 설정했으며,
- 경사하강법으로 가중치를 업데이트하는
붓꽃 분류기를 구현한 결과는 아래와 같다. 전체 4차원의 feature 중 2차원(꽃받침 길이, 꽃잎 길이)만을 feature로 사용했다.
N = 150 # number of samples per class
D = 2 # feature dimension
K = 3 # number of classes
reg = 0.05 # regularization strength
eta = 0.05 # learning rate
# initialize weights (and bias)
W = np.random.randn(D, K) * 0.01
b = np.zeros(K)
# training process
losses = []
for epoch in range(1000):
# construct linear decision function
s = X.dot(W) + b
# compute gradients (backpropagation / chain rule)
p = np.exp(s) / np.sum(np.exp(s), axis=1, keepdims=True)
I = np.zeros(p.shape)
I[range(X.shape[0]), y] = 1
df = (p - I) / X.shape[0]
dW = (X.T).dot(df)
dW += reg * W
db = np.sum(df, axis=0)
# update weights by gradient descent
W -= eta * dW
b -= eta * db
# calculate and print loss
data_loss = -np.sum(np.log(p[range(X.shape[0]), y])) / X.shape[0]
reg_loss = np.sum(0.5 * reg * (W**2))
loss = data_loss + reg_loss
losses.append(loss)
if epoch % 100 == 0:
print "{}: loss={}".format(epoch, loss)
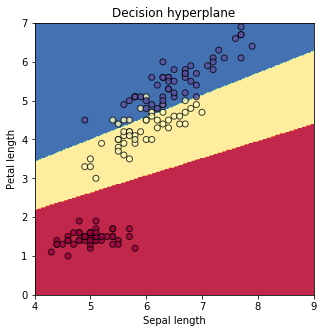
그림의 각 데이터 포인트의 색은 진짜 붓꽃 종, 배경에 칠해진 색은 선형 분류기가 예측한 각 붓꽃 종의 영역이다. 그 결과 92.7%의 accuracy를 획득할 수 있었다.
(편의상 training set, testing set, validation set을 분리하지 않고 모든 데이터를 학습시켰다. 제대로 구현하고 성능평가 하려면 학습 전 데이터셋 분리부터 해야한다.)
비선형 분류기의 필요성
현실의 데이터가 직선적으로 분류 가능한 경우는 매우 드물다. 직선으로 구획하기 어려운 데이터에서 선형 분류기의 성능은 정말이지 처참하다.
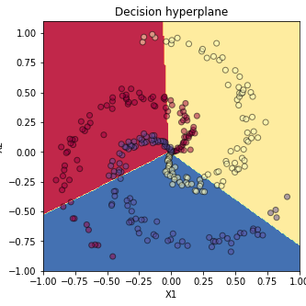
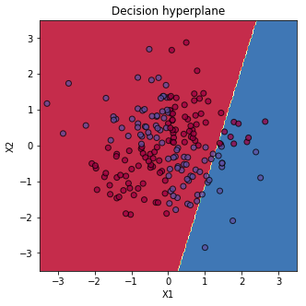
커널 트릭(kernel trick) 등 학습 데이터를 변형하는 방법을 포함해 비선형 데이터를 효과적으로 분류-예측하기 위해 다양한 방법들이 연구되어왔다. 이 글 시리즈의 핵심 개념인 ANN 역시 비선형 함수를 표현하기 위해 고안된 방법 중 하나다.
다음 글에서는 직선적이지 않은 분류 문제를 다루는 것으로 시작해서 신경망의 개념과 함께 신경망을 이용한 간단한 비선형 분류기를 구현하기까지를 건드려보겠다.
참고
- 이 글은 CS231n 강의록을 많이 참고했다. 원 강의록을 읽어보시기를 추천드린다.
- 선형 분류기를 구현한 노트북은 여기에서 다운받을 수 있다.