인공신경망 이해하기 (4) 학습 과정 - 디테일

Apr 20, 2018 • Sihyung Park
machine learning  

$\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}$ $\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}$

지금까지의 글에서는 머신러닝의 기초와 신경망의 구조 및 학습에 대해서 다루어보았다. 그러나 중간중간 “추후에 기회가 된다면 자세히 다루겠다”고 미뤄둔 내용들이 있다.

이번 글에서는 지금까지 다룬 뼈대에 살점을 붙여보려고 한다. 자주 등장하는 개념을 위주로 정리해보려 했다. 여기서부터는 신경망을 포함한 머신러닝 학습의 디테일이다.

• 정규화
  • Ridge 정규화 ($\ell_2$ 정규화)
  • Lasso 정규화 ($\ell_1$ 정규화)
  • Elastic Net 정규화
  • 그래서 뭘 써야하나요
  • Dropout
  • DropConnect
• 수치적 최적화
  • 일반 경사하강법
  • 모멘텀 경사하강법
  • Nesterov 모멘텀 경사하강법
  • 적응형 학습률(adaptive learning rate) 방법
• 데이터 전처리
  • 센터링(centering)과 스케일링(scaling)
  • Minmax 표준화
  • 주성분 분석 (Principal Component Analysis; PCA)
• 참고

정규화

정규화의 개념과 학습에서의 역할에 대해서는 이전 글에서 언급했었다. 간단히 다시 정리하자면, 분류기가 데이터에서 분류문제와 상관이 없는 노이즈까지 학습하지 않도록 제약을 두는 것을 말한다.

정규화 방법들의 디테일에 대해서 살펴보기 전에 가중치 행렬과 편향 벡터를 다시 들여다보자. 다음은 신경망의 한 층만을 식으로 나타낸 것이다. 선형 분류기의 판별함수와도 같은 식이다.

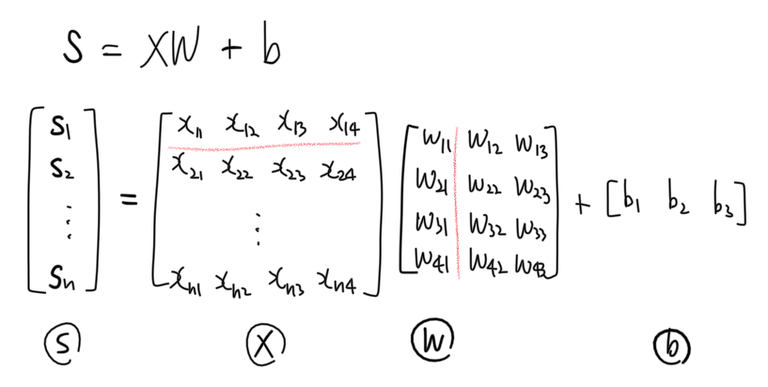
스케치 재활용 장난아니다..는 생각은 접어두고, 이 식 $XW + b$은 다음과 같이 더욱 간단히 줄일 수 있다. 두 식의 계산 결과는 완전 동일하다.

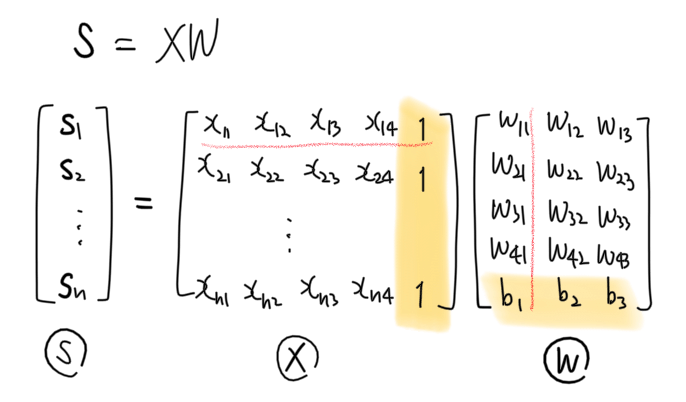
무슨 짓을 한걸까? feature 행렬 $X$의 열에 1열벡터를 추가해주었고 가중치 행렬 $W$와 편향 벡터 $b$를 합쳐서 하나의 큰 가중치 행렬로 만들었다. 이처럼 feature 행렬의 마지막 열에 1벡터를 추가해서 가중치와 편향을 하나의 벡터로 나타내는 기술을 “feature 행렬을 증강시킨다 (feature matrix augmentation; design matrix augmentation)“고 한다.

표기 및 구현상의 편의성을 이유로 실제 알고리즘을 코딩할 때는 증강된 버전을 많이 사용한다. 이제부터 말하는 가중치 행렬 $W$는 모두 증강된 가중치 행렬이다. 즉, 가중치 $w_{ij}$ 뿐만 아니라 편향 정보 $b_k$도 포함하고 있는 행렬이다. 편의상 편향 정보도 $w_{ij}$라고 호칭하겠다.

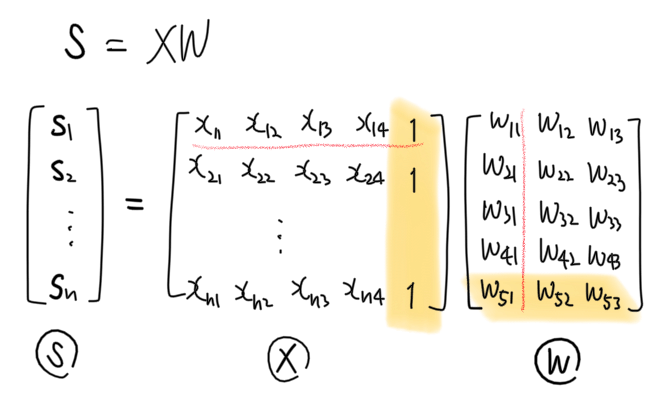
이제 우리의 가중치 행렬은 이렇게 생겼다.

Ridge 정규화 ($\ell_2$ 정규화)

이미 선형 분류기를 구현하는 과정에서 한 차례 다룬적이 있는 Ridge 정규화법은 가중치 행렬 $W$의 모든 성분 $w_{ij}$의 제곱합 $R(W) = \sum_{\forall (i, j)} w_{ij}^2$을 제약하는 정규화법이다. $\ell_2$ norm(제곱합)을 제약하기 때문에 l2 정규화라고도 부른다.

Ridge 정규화된 가중치행렬은 전체적으로 고르고 작은 값을 선호하게 된다. 튀는 값이 있거나 전체적으로 가중치의 크기가 커지면 정규화 손실 $R(W)$의 값이 커진다.

Lasso 정규화 ($\ell_1$ 정규화)

가중치의 제곱합 $\sum_{\forall (i,j)} w_{ij}^2$을 제약하는 Ridge 정규화와 달리 Lasso 정규화는 가중치의 절대값의 합 $R(W) = \sum_{\forall (i,j)} |w_{ij}|$을 제약한다. $\ell_1$ norm(절대값의 합)을 제약하기 때문에 $\ell_1$ 정규화라고도 널리 불린다.

Lasso 정규화된 가중치행렬은 중요한 feature에 연결된 가중치값을 제외하고는 작은 가중치값을 가지도록 제약하는 경향이 있다. 그래서 Lasso 정규화 강도를 점차 늘리면 가중치값이 분류 문제 해결에 덜 중요한 feature 순서대로 0이 되는 것을 확인할 수 있다. 이를 플롯해보면 다음과 같다.

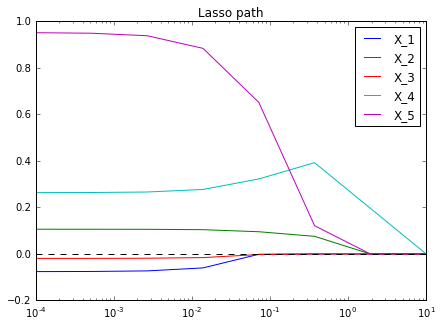
각 feature에 대응하는 가중치값이 0으로 수렴하는 속도를 보여주는 이 플롯을 Lasso path라고 한다. 선형 분류기나 회귀분석에서는 Lasso path를 사용해서 feature 중요도를 판단하기도 한다. 더 천천히 0이 되는 가중치의 feature일수록 더 중요한 feature인 것이다. 그림의 경우는 $X_4$가 가장 중요한 feature라고 판단할 수 있다.

Elastic Net 정규화

1차항(Lasso)과 2차항(Ridge)을 모두 사용해서 정규화를 할 수도 있다.

$R(W) = \alpha \sum_{\forall (i,j)} w_{ij}^2 + (1-\alpha) \sum_{\forall{(i,j)}}

w_{ij}

$

여기서 $\alpha$는 [0, 1] 구간 내의 값으로 1차항 제약과 2차항 제약 사이의 밸런스를 조정하는 역할을 한다. $\alpha=0$일 때는 Lasso 정규화와 동일해진다 (2차항 정규화항이 0이 되어 사라진다). 반대로 $\alpha=1$일 때는 Ridge 정규화와 동일해진다 (1차항 정규화항이 0이 된다).

그래서 뭘 써야하나요

셋 중 무슨 정규화를 사용할지 고민이라면 일단은 Ridge를 쓰면 된다. 튀는 값을 불호하는 Ridge의 특성상 덜 공격적인 가중치값을 얻을 수 있다.

신경망 모형의 경우엔 주로 Ridge 정규화와 함께 아래에서 설명할 Dropout 기법을 사용해서 정규화한다.

Dropout

지금껏 설명한 다른 정규화법과 달리 Dropout은 신경망 기반 모형에 특화된 정규화 방법이다. Dropout의 직관은 이렇다: 각각의 뉴런은 매 학습에서 $p$의 확률로 활성화될 수도 있고 그렇지 않을 수도 있다.

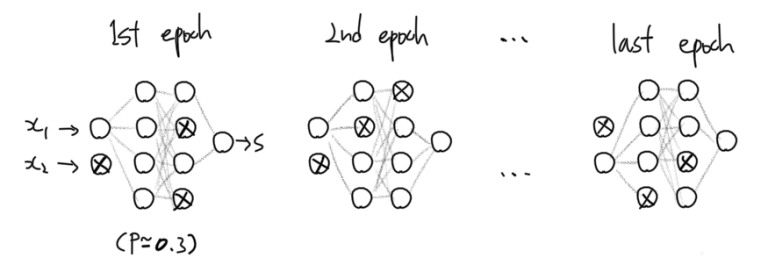
이렇게 학습시킨 신경망의 분류결과는 마치 비슷하지만 서로다른 여러개의 신경망 모형들의 분류 결과를 평균내는 것과 유사한 형태가 된다. 신경망 여러개의 결과가 평균내졌기 때문에 일반적이지 않은 분류 결과를 제거하는 정규화의 효과를 가진다.

Dropout을 사용하면 학습 과정에서 각 뉴런의 활성화 확률이 $p$이므로 활성화 기댓값은 $E(a) = p \times f(XW) + (1-p)\times0 = p \times f(XW)$이다. 즉, Dropout을 사용하지 않았을 때의 활성화함수값 $f(XW)$에 비해 크기가 $p$의 비율로 작아진다.

Test set에서 성능평가를 할 때에는 모든 뉴런이 활성화된 상태에서 분류를 하므로 활성화함수값을 학습할 때와 같은 크기로 조정해줘야 한다. 성능평가시의 활성화함수값에 $\times p$를 해주면 학습시의 활성화함수값과 같은 크기로 조정된다.

Test set에서 성능평가시에 활성화함수값의 크기를 조정해줘야하는 귀찮음때문에 새로운 방법이 고안되었다. 새로운 방법에서는 활성화함수값의 크기를 학습시에 $\div p$로 조정해준다. 이렇게 하면 학습시 활성화함수의 기댓값은 $E(a) = {p \times f(XW) + (1-p)\times0} \div p = f(XW)$가 되므로, 성능평가시에는 별도의 활성화함수값 조정을 해주지 않아도 된다.

이 방식을 inverted Dropout이라고 하며, 일반적으로 dropout을 사용했다고 하면 열에 아홉은 inverted dropout을 사용했다는 말이다. inverted가 아닌 dropout은 잘 사용하지 않는다.

DropConnect

Dropout과 유사한 방법으로 DropConnect라는 방법이 있다. 매 epoch마다 랜덤하게 뉴런의 출력을 죽여버리는 Dropout과 달리 DropConnect는 매 epoch마다 뉴런의 입력을 랜덤하게 죽인다.

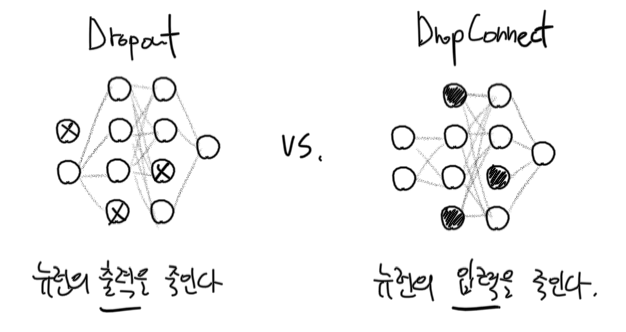
DropConnect를 사용하면 특정 뉴런을 완전히 죽이지는 않고 일부 연결만 죽일 수도 있다. 따라서 DropConnect는 Dropout을 포함하는, 더 일반적인 개념이라 할 수 있겠다.

수치적 최적화

수치적 최적화 역시 처음 선형 분류기를 학습시킬 때 언급했었다. 수치적 최적화는 손실함수값 $L$을 최소로 만드는 가중치값 $W$를 찾기 위해 사용됐었다. 지금까지는 경사하강법(또는 SGD)을 사용해서 수치적 최적화를 진행했었다.

일반 경사하강법

일반 경사하강법은 그라디언트의 반대 방향으로 가중치를 움직이며 최적의 가중치값을 찾는 방법이다.

\[W_{new} = W_{old} - \eta \frac{\partial L}{\partial W}\]

계산 시간과 메모리를 절약하기 위해서 확률적 경사하강법(SGD)를 사용할 수도 있었다. 매 학습에서 가중치 하나만으로 그라디언트를 계산하는 SGD는 아래와 같이 표현된다.

\[W_{new} = W_{old} - \eta \frac{\partial L}{\partial w_{ij}}\]

일반 경사하강법은 손실함수의 최저점 주변에서 가중치 값이 진동하는 특징이 있다.

모멘텀 경사하강법

모멘텀 경사하강법은 물리학적인 관점에서 경사하강법을 재해석한 방법이다.

손실함수 모양의 곡선에 공을 굴러 떨어뜨린다고 생각해보자. 공의 위치에너지와 운동에너지를 생각해볼 수 있다. 모멘텀 경사하강법에서는 그라디언트를 공의 위치에너지라고 생각한다. 최초의 운동에너지는 0이라고 본다.

1. 위치에너지($= \frac{\partial L}{\partial W_{old}}$)는 운동에너지 $v$로 변환된다.
   • $v_\text{new} = \mu \times v_\text{old} - \eta \frac{\partial L}{\partial W_\text{old}}$
   • 여기서 새로운 하이퍼 파라미터 $\mu$이 등장한다. $m$은 모멘텀이라고 부른다. 실제로는 마찰계수와 비슷한 역할을 한다 (업데이트 전의 속도 $v_{old}$를 감소시킨다).
2. 1.에서 업데이트된 운동에너지만큼 가중치가 움직인다.
   • $W_{new} = W_{old} + v_{new}$
3. 손실 함수가 수렴할 때까지 반복한다.

Nesterov 모멘텀 경사하강법

Nesterov는 모멘텀 경사하강법에 대한 개선법을 내놓았다.

“공”을 이미 관측한 시점에서 가속도와 속도를 계산하면, 과거의 속도를 이용해서 미래의 공의 위치를 결정하는 것이므로 진짜 현실세계에서 떨어지고 있는 공의 물리적 성질과는 약간의 차이가 있을 것이다. 따라서 굴러가는 “공”을 더 현실에 가깝게 물리학적으로 모델링하려면 앞으로 공이 움직일 위치($W_{ahead}$)와 속도($\frac{\partial L}{\partial w_{ahead}}$)를 예측해서 공의 위치(가중치값 업데이트 $W_{new}$)를 결정해야 한다.

Nesterov의 모멘텀 경사하강법은 이렇게 진행된다.

1. 가까운 미래의 공의 위치 $W_{ahead}$를 예측한다.
   • $W_{ahead} = W_{old} + (m \times v)$
2. 가까운 미래의 위치 $W_{ahead}$에서의 그라디언트(즉 위치에너지; $\frac{\partial L}{\partial W_{ahead}}$)를 계산한다.
3. 위치에너지 $\frac{\partial L}{\partial W_{ahead}}$를 운동에너지 $v$로 변환시킨다.
   • $v_{new} = \mu \times v_{old} - \eta \frac{\partial L}{\partial W_{ahead}}$
4. 운동에너지만큼 가중치를 움직인다.
   • $W_{new} = W_{old} + v_{new}$

모멘텀 경사하강법들은 일반 경사하강법에 비해 훨씬 빠른 속도로 손실함수의 최저점에 도달한다. 하지만 “관성”때문에 손실함수의 최저점이 되는 값을 지나쳐버렸다가 되돌아오는(“overthrow”되는) 성질이 있다.

적응형 학습률(adaptive learning rate) 방법

모멘텀 경사하강법이 경사를 타고 내려오는 속도를 변형시켜 개선시켰다면, 적응형 학습률 방법은 학습 도중에 학습률 $\eta$를 변형시켜서 개선시킨다 - 그래서 이름이 적응형 학습률(adaptive learning rate)이다.

적응형 학습률 방법은 매 학습에서의 그라디언트 정보를 캐시(cache)라는 변수에 차곡차곡 “기억”해둔다. 그리고 캐시를 이용해서 학습률 $\eta$를 조정해 나간다. 학습이 진행되어 그라디언트가 작아져도 학습 속도가 느려지지 않도록 조정해주며 가중치를 fine-tuning하는 데에 도움이 된다.

Adagrad라고 이름붙은 방법은 다음과 같이 학습률 $\eta$를 조정한다.

1. 그라디언트를 이용해서 캐시를 업데이트한다.
   • $\text{cache}_{new} = \text{cache}_{old} + (\frac{\partial L}{\partial w_{old}})^2$
2. 학습률 $\eta$를 조정(업데이트)한다.
   • $\eta_{new} = \frac{\eta_{old}}{\sqrt{\text{cache}_{new}}}$
3. 가중치 $W$를 업데이트한다.
   • $W_{new} = W_{old} - \eta_{new} \frac{\partial L}{\partial W}$

제프리 힌튼이 제시한 RMSProp이라는 방법에서는 캐시가 시간이 지남에 따라 정보를 조금씩 “잊어버린다”.

1. 그라디언트를 이용해서 캐시를 업데이트한다. 단, 캐시는 이전 정보의 일부를 잊어버린다. decay rate $\gamma$만큼의 정보만 기억한다.
   • $\text{cache}_\text{new} = \gamma \times \text{cache}_\text{old} + (1 - \gamma) \times (\frac{\partial L}{\partial w_\text{old}})^2$
2. 학습률 $\eta$를 조정(업데이트)한다.
   • $\eta_\text{new} = \frac{\eta_\text{old}}{\sqrt{\text{cache}_\text{new}}}$
3. 가중치 $W$를 업데이트한다.
   • $W_\text{new} = W_\text{old} - \eta_\text{new} \frac{\partial L}{\partial W}$

실제 학습 시 각 방법의 움직임 특징을 보이기 위해서 움짤을 만들어봤다.

이 애니메이션은 유명하다 (출처).

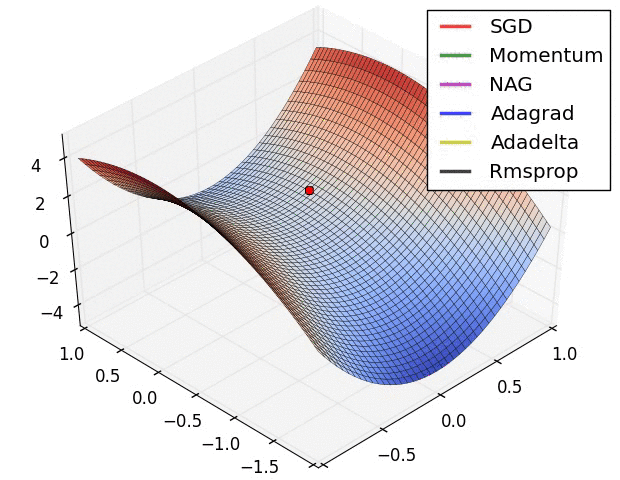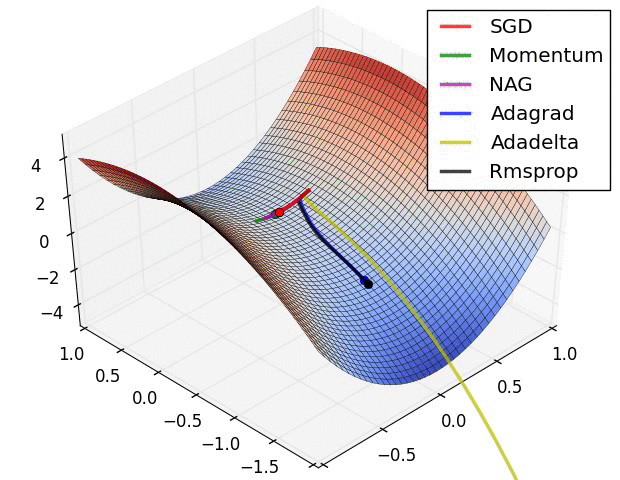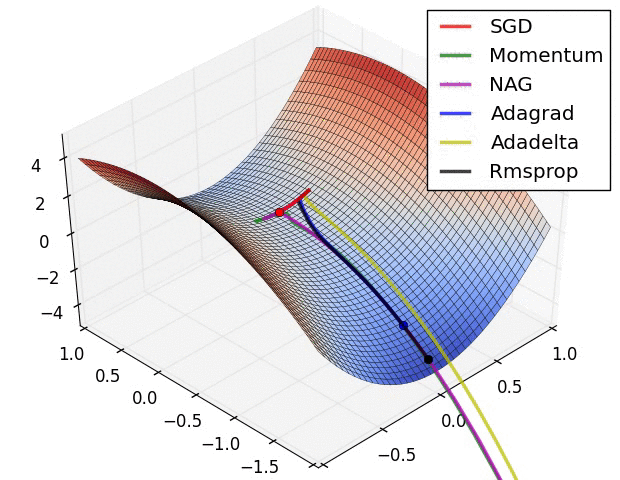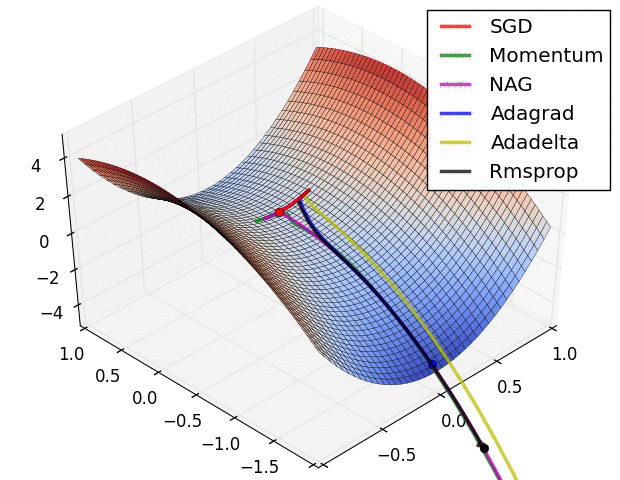
데이터 전처리

분류기에 학습을 시키기 전에 입력 데이터를 학습에 알맞게 변형시키는 과정을 일컬어 전처리(preprocessing)라 부른다. 전처리는 주로 학습 데이터의 본질만을 남겨두고, 학습에 방해가 되는 요소를 제거하는 역할을 한다.

예를 들어 붓꽃 분류 문제에서, 꽃받침 길이는 cm 단위로 측정되어 있는데 꽃받침 너비는 mm 단위로 측정되었다면 어땠을까? mm 단위로 측정된 값들이 대체로 cm 단위로 측정된 값보다 큰 수치로 기록되어 있을 것이고 이는 가중치의 업데이트에 좋지 않은 영향을 미칠 것이다.

전처리 과정에서는 이처럼 단위 차이에 의한 영향, 최대최소값의 차이에 의한 영향, 평균값의 차이에 의한 영향, 분포도 차이에 의한 영향 등 데이터의 본질과는 무관한 영향을 제거한다.

전처리시 주의해야할 점은 전처리 통계량(데이터 평균, 데이터 분산, eigenvalue, eigenvector, …)은 모두 training set에서만 계산되어야 한다는 것이다. 이에 대해서는 이전 글에서 다루었다.

센터링(centering)과 스케일링(scaling)

가장 간편하고 보편적인 전처리는 데이터를 평균 0, 분산 1을 따르도록 변형시키는 것이다. 이 중 평균을 0으로 만드는 과정을 센터링(centering)이라고 하고 분산을 1로 만드는 과정을 스케일링(scaling)이라고 한다.

굳이 하나를 고른다면 스케일링보다는 센터링이 훨씬 중요하다고 한다.

Minmax 표준화

데이터의 분포를 유지한 채로 모든 관측값이 일정 구간 (주로 [0, 1]) 사이에 존재하도록 변형하고 싶다면 minmax 표준화를 사용할 수 있다.

$X_\text{normalized} = \frac{X - \min(X)}{\max(X) - \min(X)}$

변형한 데이터는 모두 [0, 1] 사이의 값을 갖게 된다. 이 방법은 데이터를 센터링하지는 않기 때문에 신경망에 사용하기엔 부적합할 수 있다.

주성분 분석 (Principal Component Analysis; PCA)

주성분 분석은 상관관계가 존재할 수도 있는 데이터셋을 서로 독립인 성분(주성분)의 데이터셋으로 분리해주는 테크닉이다.

PCA는 데이터의 공분산 행렬(covariance matrix) $\Sigma$을 특이값 분해(singular-value decomposition; SVD)시키는 과정과 동일하다. 혹은 데이터의 상관 행렬(correlation matrix) $R$을 고유값 분해(eigen-value decomposition)시키는 과정과 동일하다.

상관관계가 존재하는 데이터 $X$는 PCA를 통해서 세 행렬의 곱으로 분해할 수 있다.

\[X = Z_s D^{1/2} U^T,~ Z_s = XUD^{-1/2}\]

여기서 $Z_s$는 평균이 0이고 분산이 1이며 모든 차원이 서로 독립(full-rank)인 데이터이다. $D$는 $Z$의 각 차원의 분산의 행렬이다. 동시에 $X$의 eigenvalue를 대각성분으로 가지는 대각행렬이기도 하다. $U$는 회전행렬이다. 동시에 $X$의 eigenvector matrix이기도 하다.

이를 기하적으로 해석해보면 이렇다: 모든 차원이 서로 독립이고 표준화된 데이터 $Z_s$는 차원간 상관관계가 존재하는 데이터 $X$를 $U$만큼 회전시키고 $D^{-1/2}$로 표준화시켜서 얻을 수 있다. 이 과정에서 얻은 $Z_1, Z_2$ 또는 $Z_{s_1}, Z_{s_2}$를 주성분(principal component; PC)라고 부른다.

데이터를 센터링, 스케일링하는 대신 PCA 후 PC를 사용해도 된다. 한 차원의 PC만으로도 대부분의 데이터 분산을 설명할 수 있다면 아예 데이터의 차원을 축소해도 된다. 그림의 경우 $Z_1$만으로도 대부분의 데이터 분산을 설명할 수 있으므로 $Z_2$ 차원을 버리고 1차원으로 데이터를 축소시켜도 된다.

주저리 주저리 설명하긴 했지만 신경망 모형에서는 주로 PCA보다 센터링 + 스케일링을 선호한다고 한다.

여기까지 Batch Normalization 하나만 빼고 대강의 살은 붙였다. 다음 글에서는 신경망에 적용시킬 수 있는 특수한 층(layer) 구조에 대해서 다뤄보겠다.

참고

• 이 글은 CS231n 강의록을 많이 참고했다. 원 강의록을 읽어보시기를 추천드린다.
• Adaptive learning rate method 내용은 이 페이지를 참고했다.
• 첫 번째 수치적 최적화 비교 GIF를 만드는 과정에서 최적화할 함수 모양을 설정할 때 이 페이지를 참고했다.
• 두 번째 수치적 최적화 비교 GIF는 CS231n에서 가져왔으나 원 출처는 여기다.
• PCA 내용은 “Analyzing Multivariate Data” (Lattin et al., 2002)를 참고했다.