2. Univariate Kernel Density Estimation
From histogram, we will start discussing nonparametric kernel methods.
Problem setting
$X_1,\cdots,X_n \in \mathbb{R}$ are i.i.d. random variables with density $p$ with respect to the Lebesgue measure. Our goal is to estimate $p$ with the data $\{X_1, \cdots, X_n\}.$ Note that this problem is ill-defined: No element in the class $\{p: p\ge 0, \int p = 1\}$ maximizes $\prod_{i=1}^n p(X_i).$
Suppose there exists a maximizer $p.$ Let $p'$ be a density that has greater mass than p along the region containing $X_i,$ then $\prod_{i=1}^n p'(X_i) > \prod_{i=1}^n p(X_i).$
Histogram
Histogram is probably the most intuitive and simple approach to nonparametric density estimation.
Let $B_j$ be the $j$th bin. i.e. $\{B_j\}_j$ is a partition of $\mathbb{R}.$ Let $b_j$ be the width of the $j$th bin. Then $$\begin{aligned} \hat p(x) &= \frac{1}{nb_j} \sum_{i=1}^n \mathbf{1}_{B_j}(X_i),~ x \in B_j \\ &= \frac{1}{nb_j} \sum_{i=1}^n \sum_{i=1}^n \sum_j \mathbf{1}_{B_j} (X_i) \mathbf{1}_{B_j}(x). \end{aligned}$$ is the histogram estimator of $p.$
Motivation
We can think of relative frequency as a density estimation method.
\[\begin{aligned} p(x) &\approx \frac{1}{n}(\text{frequency of $B_j$}) \\ &\approx \mathbb{P}(X_1 \in B_j), ~~~~~~~~~~~ (1) \\ &= \int_{B_j} p(u)du \\ &\approx p(x) \cdot b_j, ~~~~~~~~~~~~~~~~\:\; (2) \end{aligned}\]Here, (1) gives bad approximation if $b_j$ is too small relative to $n$. This is because frequency of $B_j$ merely becomes 0. On the other hand, (2) gives bad approximation if $b_j$ is too large, since the density is estimated by a constant function at its extreme.
Maximum likelihood property
Let
\[\begin{aligned} \mathcal{F} &= \left\{p: p\ge0, \int p = 1, p=c_j \text{ on } B_j, c_j \in \mathbb{R}\right\} \\ &= \left\{\sum_{j=1}^\infty c_j\cdot\mathbf{1}_{B_j}: c_j \ge 0, \sum_{j=1}^\infty b_jc_j = 1\right\}. \end{aligned}\]Then $\hat p = \argmax_{f \in \mathcal{F}} \prod_{i=1}^n p(X_i).$ That is, histogram is the maximizer of likelihood among the step functions.
$$ \begin{aligned} \ell(p) &= \sum_{i=1}^n \log p(X_i) \\ &= \sum_{i=1}^n \log \left( \sum_{j=1} c_j \mathbf{1}_{B_j}(X_i) \right) \\ &= \sum_{j=1}^\infty \sum_{i=1}^n \mathbf{1}_{B_j}(X_i) \log{c_j} \\ &= \sum_{j=1}^\infty f_j\log c_j,~ f_j := \sum_{i=1}^n \mathbf{1}_{B_j}(X_i)\\ &=: \ell(c_1,c_2,\cdots) \end{aligned} $$ $$ \text{Maximize } \ell(c_1,\cdots) \text{ subject to } \sum_{j=1}^\infty b_jc_j = 1,~ c_j \ge 0. \\ \iff \text{Maximize } \ell(a_1,\cdots) \text{ subject to } \sum_{j=1}^\infty a_j = 1,~ a_j \ge 0. \\ \implies \begin{cases} f_j=0,&~ a_j=0 \text{ maximizes } \ell &\Rightarrow c_j=0 \\ f_j>0,&~ a_j > 0 &\Rightarrow c_j\ne0 \end{cases} $$ Let $f_{(1)}, \cdots, f_{(k)} > 0$ be the subset of $\{f_j\}$ with positive values only. Then $$ \begin{aligned} \ell(c_1,\cdots) &= \ell(c_{(1)}, \cdots, c_{(k)}) \\ &= \sum_{i=1}^k f_{(i)} \log c_{(i)} \\ &= \sum_{i=1}^{k-1} f_{(i)} \log c_{(i)} + f_{(k)} \log\left( 1 - \sum_{i=1}^{k-1} c_{(i)} \right) \end{aligned} $$ Checking the second order optimality we get $$ \hat c_{(i)} = \frac{f_{(i)}}{nb_{(i)}},~ i=1,\cdots,k. $$
Error analysis
For function estimation, we frequently use mean integrated squared error (MISE) as an error metric. MISE is defined as follows:
\[\begin{aligned} \text{MISE}(\hat p) &:= E\int \left(\hat p(x) - p(x)\right)^2 dx \\ &= \int \text{MSE}(\hat p(x)) dx. \end{aligned}\]The second inequality follows from Fubini’s theorem, because the integrand is clearly non-negative.
Since MSE can be decomposed into squared bias and variance, in order to get a sense of MISE, it is helpful to compute bias and variance of $\hat p(x).$ To simplify the process, we assume $b_j=h$ for all $j$ and $B_j = [(j-1)h,~ jh).$ Let $j(x)$ be the index of the bin where $x$ belongs. That is, $x \in B_{j(x)}.$ Then as $h \to 0$ and $nh\to\infty$ as $n \to \infty,$1 we get
$$ \begin{aligned} \text{bias}(\hat p (x)) &= p'\left((j(x) - \frac{1}{2})h \right) \left\{ (j(x) - \frac{1}{2})h - x \right\} + o(h), \\ \text{Var}(\hat p(x)) &= \frac{1}{nh}p(x) + o\left(\frac{1}{nh}\right) \end{aligned} $$
Since $f_j \sim \mathcal{B}(n, \mathbb{P}(X_1 \in B_j)),$ we get $$ E\hat p(x) = \frac{1}{nh}n\mathbb{P}(X_1 \in B_j) = \frac{1}{h} \int_{(j-1)h}^{jh} p(x)dx, $$ where $j = j(x).$ Thus $$ \begin{aligned} \text{bias}(\hat p(x)) =& \frac{1}{h} \int_{(j-1)h}^{jh} p(t)-p(x)~dt \\ =& \frac{1}{h} \int_{(j-1)h}^{jh} (t-x)p'(x)~dt + (t-x)\int_0^1 p'(x+u(t-x)) - p'(x) ~du~dt \\ =& \frac{1}{h} \int_{(j-1)h}^{jh} (t-x)p'(x)~dt + \int_0^1 \int_{(j-1)h}^{jh} \frac{t-x}{h} \{p'(x+u(t-x)) - p'(x)\} ~dt~du \\ =& \left((j-\frac{1}{2})h - x\right) p'(x) + \int_0^1 \int_{(j-1)h}^{jh} \frac{t-x}{h} \{p'(x+u(t-x)) - p'(x)\} ~dt~du \\ =& \left((j-\frac{1}{2})h - x\right) p'\left((j-\frac{1}{2})h\right) \\ &+ \int_0^1 \int_{(j-1)h}^{jh} \frac{t-x}{h} \{p'(x+u(t-x)) - p'(x)\} ~dt~du \\ &+ o(h). \end{aligned} $$ We get the desired result since $$ \begin{aligned} |(\text{2nd term})| &\le \int_0^1 \int_{(j-1)h}^{jh} \left|\frac{t-x}{h}\right| \left|p'(x+u(t-x)) - p'(x)\right| ~dt~du \\ &\le \int_0^1 \int_{(j-1)h}^{jh} 1 \cdot \sup_{|y|<h}|p'(x+u(t-x)) - p'(x)| ~dt~du \\ &= h \cdot \sup_{|y|<h} |p'(x+y) - p'(x)| \\ &= o(h). \end{aligned} $$ For variance, derivation is easier. $$ \begin{aligned} \text{Var}(\hat p(x)) &= \frac{1}{n^2h^2} \text{Var}(f_j) \\ &= \frac{1}{nh^2} \mathbb{P}(X_1 \in B_j) \left(1 - \mathbb{P}(X_1 \in B_j) \right) \\ &= \frac{1}{nh}\frac{1}{h} \int_{(j-1)h}^{jh} p(x)dx \cdot (1 - o(1)) \\ &= \frac{1}{nh}(p(x) + o(1))(1 - o(1)) \\ &= \frac{1}{nh}p(x) + o\left(\frac{1}{nh}\right). \end{aligned} $$
From this, we can guess MISE to be somewhat similar to \(\frac{1}{nh} + \frac{1}{12}h^2 \int (p')^2 + o\left(\frac{1}{nh} + h^2\right).\) In fact, this is the MISE of histogram estimator. However the formal derivation requires a little more than sum of MSE.
$$ \begin{aligned} \int \text{bias}^2(\hat p(x))dx &= \sum_{k\in\mathbb{Z}} \int_{B_k} \text{bias}^2 (\hat p(x)) dx \\ &= \sum_{k\in\mathbb{Z}} \int_{B_k} \left( (k-\frac{1}{2})h - x \right)^2 \left( p'\left((k-\frac{1}{2})h - x\right) \right)^2 dx + o(h^2) \\ &= \sum_{k\in\mathbb{Z}} \left(p'\left( (k-\frac{1}{2})h \right)\right)^2 \int_{B_k} \left( (k-\frac{1}{2})h \right)^2 dx + o(h^2) \\ &= \sum_{k\in\mathbb{Z}} \left(p'\left( (k-\frac{1}{2})h \right)\right)^2 \int_{(k-1)h}^{kh} \left( (k-\frac{1}{2})^2h^2 - 2(k-\frac{1}{2})hx + x^2 \right) dx + o(h^2) \\ &= \frac{1}{12}h^3 \sum_{k\in\mathbb{Z}} \left(p'\left( (k-\frac{1}{2})h \right)\right)^2 + o(h^2) \\ &= \frac{1}{12}h^3 \sum_{k\in\mathbb{Z}} \frac{1}{h} \int_{B_k} (p'(x))^2 dx + o(h^2) \\ &= \frac{1}{12}h^2 \int (p')^2 + o(h^2). \end{aligned} $$ $$ \begin{aligned} \int \text{Var}(\hat p(x)) dx &= \sum_{k\in\mathbb{Z}} \int_{B_k} \text{Var}(\hat p(x)) dx \\ &= \sum_{k\in\mathbb{Z}} \int_{B_k} \frac{1}{nh^2}\mathbb{P}(X_1 \in B_k) (1 - \mathbb{P}(X_1 \in B_k)) dx \\ &= \sum_{k\in\mathbb{Z}} \frac{1}{nh} \mathbb{P}(X_1 \in B_k) (1 - \mathbb{P}(X_1 \in B_k)) \\ &= \frac{1}{nh} \left( 1 - \sum_{k\in\mathbb{Z}} \mathbb{P}(X_1 \in B_k)^2 \right) \\ &= \frac{1}{nh} + o\left(\frac{1}{nh}\right). \end{aligned} $$ Thus the desired result follows.
We call the MISE without the approximated term the approximate MISE (AMISE). By the first order optimality condition, we can easily check that \(h_\text{opt} = \left( \frac{6}{n \int (p')^2} \right)^{1/3}\) maximizes AMISE of $\hat p.$
A parametric model have MISE $\sim n^{-1}$ if the model assumption is correct, and $\sim n^0$ otherwise. Under $h_\text{opt},$ $\text{AMISE}(h_\text{opt}) \sim n^{-2/3}$ and also $\text{MISE}(h_\text{opt}) \sim n^{-2/3}$. Comparing to a parametric approach, this is an improvement since it provides similar error rate without any model assumption.
Problems and remedies
In this section, we will cover two intrinsic problems that histogram estimator has and remedies of it, which will be a bridging concept to kernel smoother.
corner effect
Corner effect states that histogram estimates that the density at the corners of each bin is the same as in the midpoint. This takes place because a histogram estimates density as a constant inside every bins. To address the problem, we estimate density around $x$ by thinking of a bin centered at $x.$
\[\begin{aligned} \hat p(x) &= \frac{1}{nh} \sum_{i=1}^n \mathbf{1}_{(x-h/2,~x+h/2)}(X_i) \\ &= \frac{1}{n} \sum_{i=1}^n \frac{1}{h} \mathbf{1}_{(-1/2,~1/2)} \left( \frac{x-X_i}{h} \right). \end{aligned} \tag{1}\]Bin edge effect
Bin edge effect states that even if we use the exactly same data and same $h$ for density estimation, estimators differ if locations of bins are different.
To solve the problem, average shifted histogram (ASH) was developed. AST is an average of $m$ different histograms with same data and same $h$, but with $\frac{h}{m}$-shifted bins.
\[\begin{aligned} A_{j,l} &:= \bigg[(j-1)h + l\frac{h}{m},~ jh + l\frac{h}{m}\bigg),\\ \hat p_{m,l}(x) &:= \frac{1}{nh} \sum_{i=1}^n \sum_{j\in\mathbb{Z}} \mathbf{1}_{A_{j,l}}(x) \mathbf{1}_{A_{j,l}}(X_i),~ 0\le l \le m-1, \\ \hat p_m(x) &:= \frac{1}{m} \sum_{l=0}^{m-1} \hat p_{m,l}(x). \end{aligned}\]$\hat p(m)$ is the $m$-ASH. It is known that as $m \to \infty,$
\[\hat p_m(x) \to \frac{1}{nh} \sum_{i=1}^n \left(1 - \left|\frac{x-X_i}{h}\right|\right) \mathbf{1}\left(\left|\frac{x-X_i}{h}\right| < 1\right). \tag{2}\]Kernel smoother
Motivation
Note that both $(1)$ and $(2)$ can be represented in the form
\[\hat p(x) = \frac{1}{n} \sum_{i=1}^n \frac{1}{h}K\left(\frac{x-X_i}{h}\right),\]where for $(1),$ $K(x) = \mathbf{1}_{(-1/2,~ 1/2)}(x)$ and for $(2),$ $K(x) = (1-|x|)\mathbf{1}(|x|<1).$ What if we use a function $K$ that can generalize the family of functions of interest and better estimates density?
Kernel density estimator
A kernel density estimator is defined as
\[\begin{aligned} \hat p(x) &= \frac{1}{n} \sum_{i=1}^n \frac{1}{h}K\left(\frac{x-X_i}{h}\right) \\ &= \frac{1}{n} \sum_{i=1}^n K_h(x-X_i), \end{aligned}\]where $K_h(x) := \frac{1}{h}K(\frac{x}{h}).$ Here we call $h$ a bandwidth and such function $K$ (or $K_h$) a kernel function. Usually kernel functions are set to be symmetric and satisfy $\int K(x)p(x)dx = 1$ for $\int \hat p(x)dx = 1.$
Support of $K$ determines the local region of averaging. For instantce, if $\text{supp.}K = [-1,1],$ then $\hat p(x)$ is the local weighted average on data $X_i$’s inside the interval $[x-h,~x+h].$
Error analysis
Since the expectation of $\hat p(x)$ is a convolution of $K_h$ and $p(x)$:
\[\begin{aligned} E\hat p(x) &= E K_h(x-X_1) \\ &= \int K_h(x-u)p(u)du \\ &= K_h * p(x), \end{aligned}\]expansion of $K_h * p(x)$ would be helpful for error analysis.
(A1) $p$ is $r$ times continuously differentiable at $x$, and $p^{(r)} \in L^1.$
(A2) $|u|^{r+1} K(u) \to 0$ as $|u| \to \infty,$ and $\int |u|^r K(u) du < \infty.$
Then as $h \to 0,$ $$ K_h * p(x) = \sum_{j=1}^r \frac{(-1)^j h^j}{j}\mu_j(K) p^{(j)}(x) + o(h^r), $$ where $\mu_j(K) := \int u^j K(u)du.$
If $\text{supp.}K$ is compact, (A2) is automatically true. Note that $\mu_0(K) = 1$ if $\int K =1$ and $\mu_1(K) = 0$ if $K$ is symmetric. Thus in most cases, second-order expansion is enough.
(A3) $\iff$ (A1) with $r=2.$
(A4) $\iff$ (A2) with $r=2$, and $\int K = 1$ and $K$ is symmetric.
Then as $h \to 0,$ $$ \text{bias}(\hat p(x)) = \frac{1}{2} h^2 \mu_2(K)p''(x) + o(h^2). $$
This follows from the expansion theorem. The bias of KDE is of order $\mathcal{O}(h^2)$ which is far smaller than histogram’s $\mathcal{O}(h).$
(A5) $p$ is continuous at $x$.
(A6) $|u|K(u) \to 0$ as $|u|\to\infty,$ and $\int K^2 < \infty.$
Then as $h\to0$ and $nh\to\infty$ as $n\to\infty,$ $$ \text{Var}(\hat p(x)) = \frac{1}{nh} \mu_0(K^2)p(x) + o\left(\frac{1}{nh}\right). $$
Similar to histogram, we can derive MISE.
Thus
\[\text{MISE}(\hat p;h) = \frac{1}{4}h^4 \mu_2(K)^2 \int (p'')^2 + \frac{1}{nh} \int K^2 + o\left(\frac{1}{nh}\right).\]By differentiating MISE with respect to $h$ and setting it to zero, we get the maximizer
\[h_\text{opt} = \left( \frac{\int K^2}{\mu_2(K)^2 \int (p'')^2} \right)^{1/5} n^{-1/5},\]and
\[\text{MISE}(h_\text{opt}) = \frac{5}{4} \left( \mu_2(K) \left( \int K^2 \right)^2 \right)^{2/5} \left( \int (p'')^2 \right)^{1/5} n^{-4/5} + o(n^{-4/5}).\]We get a noticebly lower $\sim n^{-4/5}$ order of error compared to $\sim n^{-2/3}$ of histogram.
Optimal kernel function
Along with $h_\text{opt},$ we can further maximize MISE by selecting the best $K.$ The following two lemmas are useful for derivation of such $K.$
(i) $\mu_2(K) \left(\int K^2\right)^2 = \mu_2(K_\sigma)\left(\int K_\sigma^2\right)^2$ for all $\sigma > 0.$
(ii) $K^*$ minimizes $\int K^2$ subject to $\mu_2(K)=1.$
$\;\;\;\implies K^*$ minimizes $\mu_2(K)\big(\int K^2\big)^2.$
(iii) $K^*$ minimizes $\int K^2$ subject to $\mu_2(K)=1.$
$\;\;\;\implies K_\sigma^*$ minimizes $\int K^2$ subject to $\mu_2(K)=1$ for all $\sigma > 0.$
From the two lemmas, we get the optimal kernel
\[K^* := \argmin_{K: \mu_2(K)=1,~\int K=1,~K\ge0} \int K^2\]which leads to
\(K^*(u) = \frac{3}{4\sqrt{5}} \left(1 - \frac{u^2}{5}\right) \mathbf{1}_{(-\sqrt{5},~\sqrt{5})}(u).\) By scale invariance ((i) of the first lemma), we get the Epanechnikov kernel:
\[K^*(u) = \frac{3}{4}(1-u^2) \mathbf{1}_{(-1,~1)}(u).\]Boundary problem
KDE is free of bin edge effect and corner effect, but has a problem that underestimates density at the boundary of support of $p.$ This is called the boundary problem.

Boundary problem: estimated density at left and right boundaries drops to zero even though the data are densely located.(source)
Let’s look closer into the left-bounded case. Suppose $\text{supp.}p = [0,\infty)$ and $\text{supp.}K = [-1,1].$ Let $x=\alpha h,$ $0\le \alpha < 1$ be a point close to the left boundary of the $\text{supp.}p.$ Then
\[\begin{aligned} K_h * p(x) &= \int_0^\infty K_h(x-u)p(u) du,~~ \text{substitute } w=\frac{x-u}{h} \\ &= \int_{-\infty}^\frac{x}{h} K(w) p(x-hw) dw. \end{aligned}\]Let $\alpha = x/h,$ and define the “incomplete” moment as the expansion term:
\[\mu_j(K;\alpha) := \int_{-1}^\alpha u^j K(u)du.\]Then we get an expansion theorem similar to that from unbounded density.
By the theorem, if $p’’$ is right-continuous at $0,$
\[\begin{aligned} K_h * p(x) =&\; \mu_0(K;\alpha) - h\mu_1(K;\alpha)p'(x) + \frac{1}{2}h^2 \mu_2(K;\alpha) p''(x) + o(h^2) \\ =&\; \mu_0(K;\alpha)p(0+) \\ &+ h\big( \alpha\mu_0(K;\alpha) - \mu_1(K;\alpha) \big) p'(0+) \\ &+ \frac{1}{2}h^2 \big( \alpha^2 \mu_0(K;\alpha) - 2\alpha\mu_1(K;\alpha) + \mu_2(K;\alpha) \big) p''(0) \\ &+ o(h^2). \end{aligned}\]The second equality comes from taylor expansion of $p(x)=p(\alpha h)$ at 0. Hence we get bias and variance at the boundary as follows.
\[\begin{aligned} \text{bias}(\hat p(x)) &= \begin{cases} \mathcal{O}(1),&~ \text{if } p(0+) > 0 \\ \mathcal{O}(h),&~ \text{if } p(0+) = 0,~ p'(0+) \ne 0 \\ \mathcal{O}(h^2),&~ \text{if } p(0+) > 0,~ p'(0+) = 0,~ p''(0+) \ne 0 \end{cases}\\ \text{Var}(\hat p(x)) &= \frac{1}{nh} \mu_0(K^2;\alpha)p(x) + o\left(\frac{1}{nh}\right). \end{aligned}\]One possible solution is to adjust $K$ according to $\alpha.$ Simply multiplying a linear function to $K$ might help.
\[K(u;\alpha) := \big(a(\alpha) + b(\alpha)u\big)\cdot K(u)\]Find $K(u;\alpha)$ that satisfies both
\[\begin{cases} \mu_0\big( K(\cdot;\alpha); \alpha\big) = \int_{-1}^\alpha K(u;\alpha) du = 1, \\ \mu_1\big( K(\cdot;\alpha); \alpha\big) = \int_{-1}^\alpha u K(u;\alpha) du = 0. \end{cases}\]The solution to the system
\[K(u;\alpha) = \frac{\mu_2(K;\alpha) - \mu_1(K;\alpha)u}{\mu_0(K;\alpha) \mu_2(K;\alpha) - \mu_1(K;\alpha)^2} K(u) \mathbf{1}_{(-1,~ \alpha)}(u)\]is called the boundary kernel.
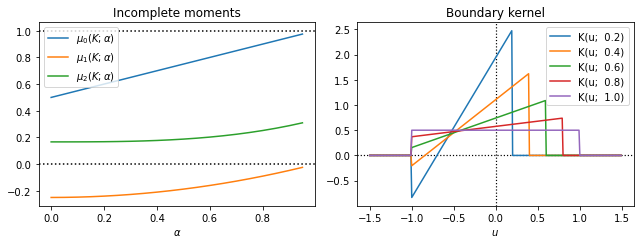
The figure above is an example of the boundary kernel. I used the simplest kernel function $K(u) = \frac{1}{2}\mathbf{1}_{[-1,~1]}$ which is the pdf of uniform distribution $\mathcal{U}[-1, 1].$ As shown, the boundary kernel gives more “weight” to each data points as $\alpha$ gets smaller.
Asymptotic normality
Given $x,$ the KDE $\hat p(x)$ asymptotically follows normal distribution.
Let $Y_{ni} = K_h(x-X_i) - K_h * p(x),$ then $$ \frac{1}{\sigma_n} \sum_{i=1}^n Y_{ni} = \frac{1}{\sqrt{\text{Var}(\hat p(x))}} \big( \hat p(x) - E\hat p(x) \big), $$ where $\sigma_n^2 = \sum_{i=1}^n \text{Var}(Y_i).$ By Lindeberg-Feller theorem, the desired result follows.
Estimation of density derivative
\[\begin{aligned} \hat p^{(r)}(x) &:= \frac{1}{nh^{r+1}} \sum_{i=1}^n K^{(r)}\left(\frac{x-X_i}{h}\right) \\ &= \frac{1}{nh^r} \sum_{i=1}^n \big(K^{(r)}\big)_h\left(\frac{x-X_i}{h}\right) \end{aligned}\]is the estimate for the $r$th derivative of $p.$
Similiar computation as before yields
\[h_\text{opt} \sim n^{-1/(2r+5)}, \\ \text{MISE}(h_\text{opt}) \sim n^{-4/(2r+5)}.\]This implies derivatives of density are much harder to estimate since deviation in $\hat p$ is amplified as $r$ increases.
References
- Nonparametric Function Estimation (Spring, 2021) @ Seoul National University, Republic of Korea (instructor: Prof. Byeong U. Park).
-
Essentially, this condition means $h$ retains to be big, but at the same time small enough relative to the growing $n.$ ↩