Quantile Normalization

•
bioinformatics  

$\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}$ $\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}$

생물정보학에서 자주 사용되는 정규화 방법 중 하나인 quantile normalization이다. Quantile normalization은 비교하려는 샘플들의 분포를 완전히 동일하게 만들고 싶을 때, 또는 기준이 되는 분포(reference distribution)가 있는 경우 샘플들의 분포를 모두 기준 분포와 동일하게 만들고 싶을 때 사용할 수 있다.

복잡한 방식을 사용하는 과정이 아닌지라 쉽게 이해하고 쉽게 써먹을 수 있다.


알고리즘

  1. 샘플 내 값을 오름차순 정렬
  2. 아래 과정을 모든 n에 대하여 반복
    1. (기준 분포가 있을 떄)
      1. 모든 샘플의 n 번째 값들을 기준 분포의 n 번째 분위수로 대체
    2. (기준 분포가 없을 때)
      1. 각 샘플의 n 번째 값들을 평균(또는 중간값)
      2. 각 샘플의 n 번째 값들을 모두 2-1.의 값으로 대체
  3. 정렬된 데이터를 원래 데이터의 순서대로 복구

이해가 어렵다면 바로 아래 “예시”로 넘어가도 된다.

“값들을 순서대로 나열했을 때 n 번째 값”이 바로 통계학에서의. n 번째 분위수(n-th quantile)의 개념에 해당하고, 각 샘플 분포의 n 번째 분위수를 동일하게 조정해주는 작업이므로 quantile normalization이라는 이름이 붙었다.

딱히 알고리즘이랄 것도 없다. 1.에서 정렬 시 오름차순 대신 내림차순을 써도 아무 상관이 없다. 기준 분포가 없을 때 2-1.에서 평균, 중간값 대신 가중평균 등 자신에게 적합한 대푯값을 사용해도 된다.


예시

1. 이해를 위한 간단한 예시

다음 테이블과 같은 세 샘플(A, B, C)의 데이터가 있다고 하자. A, B, C의 분포가 동일해지도록 median quantile normalization해보자. 셀 색상은 원래 데이터의 순서를 표시하기 위해 넣어보았다.

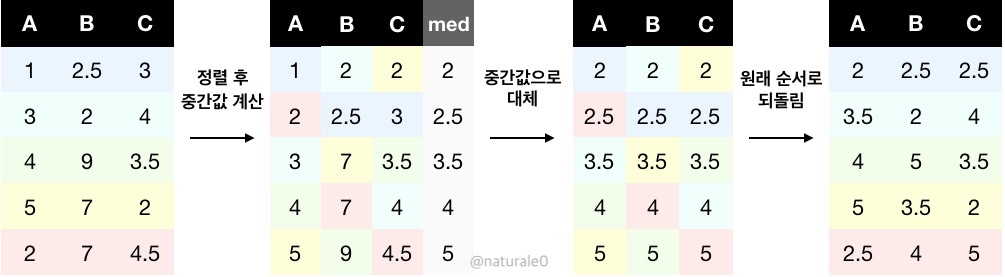
qn_whole

  1. 열 별로 값을 정렬한다.
  2. 정렬된 데이터에서 행 별로 중간값을 계산한다.
  3. 각 행의 값을 2.에서 계산한 중간값으로 바꾼다.
  4. 정렬을 해제하여 기존 데이터와 같은 순서로 돌려준다


2. 규모가 좀 더 큰 예시

서로 다른 샘플에 어떤 실험을 한 결과 데이터가 세 세트(A, B, C) 있다고 하자. 세 샘플을 용이하게 비교하기 위해 샘플의 분포를 quantile normalize하여 동일하게 만들어보자.

기준 분포가 있을 때

표준정규분포를 기준 분포로 삼는다고 하자.

정규화 전 각 샘플의 분포는 아래와 같다.

	A			B			C
0   3.570614    5.015660    6.526778
1   5.965098    1.258324    2.285988
2   3.767857    0.974910    4.374467
3   3.538398    3.362349    1.779624
4   5.178286    1.575602    3.065568
5   3.578033    3.434900    5.086503
6   5.330161    3.431059    3.573926
7   5.002079    4.885904    2.318780
8   5.694074    4.000688    4.615286
9   6.026262    -0.499165   1.999979

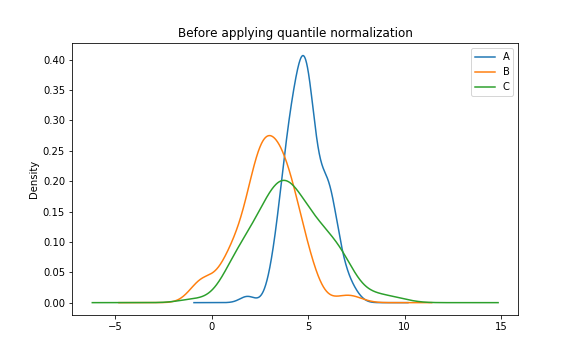
before

표준정규분포의 101-quantile을 사용하여 quantile normalization하면,

	A			B			C
0   -1.000990   1.410420    1.410420
1   0.960838    -1.180947   -1.000990
2   -0.922178   -1.346263   0.162024
3   -1.086568   0.162024    -1.232341
4   0.162024    -0.848716   -0.476577
5   -0.960838   0.263612    0.620918
6   0.289397    0.238000    -0.187224
7   -0.012409   1.232341    -0.922178
8   0.651302    0.682300    0.368003
9   1.042824    -2.330079   -1.132497

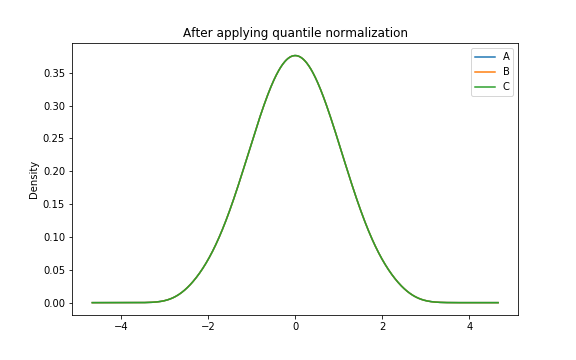
after_ref

모든 샘플의 분포가 표준정규분포와 일치하는 것을 확인할 수 있다.


기준 분포가 없을 때

기준 분포가 없이 median을 사용하여 정규화하면,

	A			B			C
0   -1.000990   1.410420    1.410420
1   0.960838    -1.180947   -1.000990
2   -0.922178   -1.346263   0.162024
3   -1.086568   0.162024    -1.232341
4   0.162024    -0.848716   -0.476577
5   -0.960838   0.263612    0.620918
6   0.289397    0.238000    -0.187224
7   -0.012409   1.232341    -0.922178
8   0.651302    0.682300    0.368003
9   1.042824    -2.330079   -1.132497

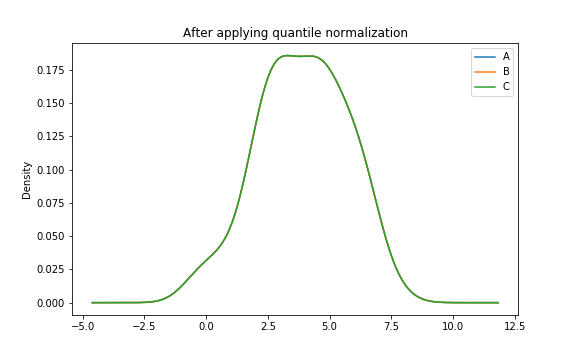
after

역시 마찬가지로 모든 샘플의 분포를 동일하게 만들 수 있다.


참고

링크한 코드를 실행하면 예시 2-2를 직접 해볼 수 있다.