The Shannon Entropy
Information theory developed by Shannon is being used not only in mathematical modeling of information transmission, but also being actively applied to ecology, machine learning and its related fields. Here, I would like to briefly review the founding concept of information theory: the Shannon entropy.
Mathematical model of communication
A communication system that we are dealing in the signal transmission can be depicted as a diagram.
The system assumes that we loses some information from the original message with probability $p(y\vert x)$ while the message is being sent through a noisy communication channel. Our goal is to reconstruct the message $\hat W$ that best guesses the $W$ sender sent.
The two essentials of communication is compression and transmission of data. We will focus on quantification of information for evaluation of methods.
For quantifying data compression, we use the Shannon entropy and rate distortion theory. For data transmission, we use mutual information and channel capacity.
Motivation for statisticians
Why do we care about communication when our interest is in statistics? Consider a supervised classification problem. Using the communication theory framework, we can interpret the learner as an auto-encoder. Then one can think of the target class $y$ as an original message. The learner can be seen as being consists of encoder and decoder part. Using the training data, the learner updates the encoder/decoder to estimate the label $\hat y.$ In this sense, the information theory achieves close relationship with statistical learning theory.
Coding theory
Notation
- $M_i$: the $i$th message
- $X_i$: the $i$th code corresponding to $M_i$
- $\ell_i$: the length of $X_i$
- $p_i$: the relative frequency of $M_i$
Vector or matrix versions of the above will be denoted by bold typeface (e.g. $\mathbf X$).
Problem setup
For efficient communication through computers, we need to encode the message into bit codes (consists of 0 or 1). There may be many ways to encode the message. For example, consider four messages $M_1$ through $M_4.$
| singular | non-singular | uniquely decodable | instantaneous | |
|---|---|---|---|---|
| $M_1$ | 0 |
0 |
10 |
0 |
| $M_2$ | 1 |
01 |
00 |
10 |
| $M_3$ | 1 |
10 |
11 |
110 |
| $M_4$ | 0 |
010 |
110 |
111 |
A Singular encoding is the one that cannot be inversed to decode the message. In constrast, a non-singular encoding is a one-to-one correspondence between the message and the code.
In the example, notice that in three-bit representation, 10 might be misinterpreted to 010. A uniquely decodable encoding is the method that does not allow such situation. Furthermore, an instantaneous encoding allows instantaneous decoding of the message. Notice that unlike the codes in the third column, receiving each bit allows one to instantly differentiate one message from others.
Clearly, the instantaneous one is the best among the four. The next question is: How can we construct such encoding? We uses a binary tree for this.
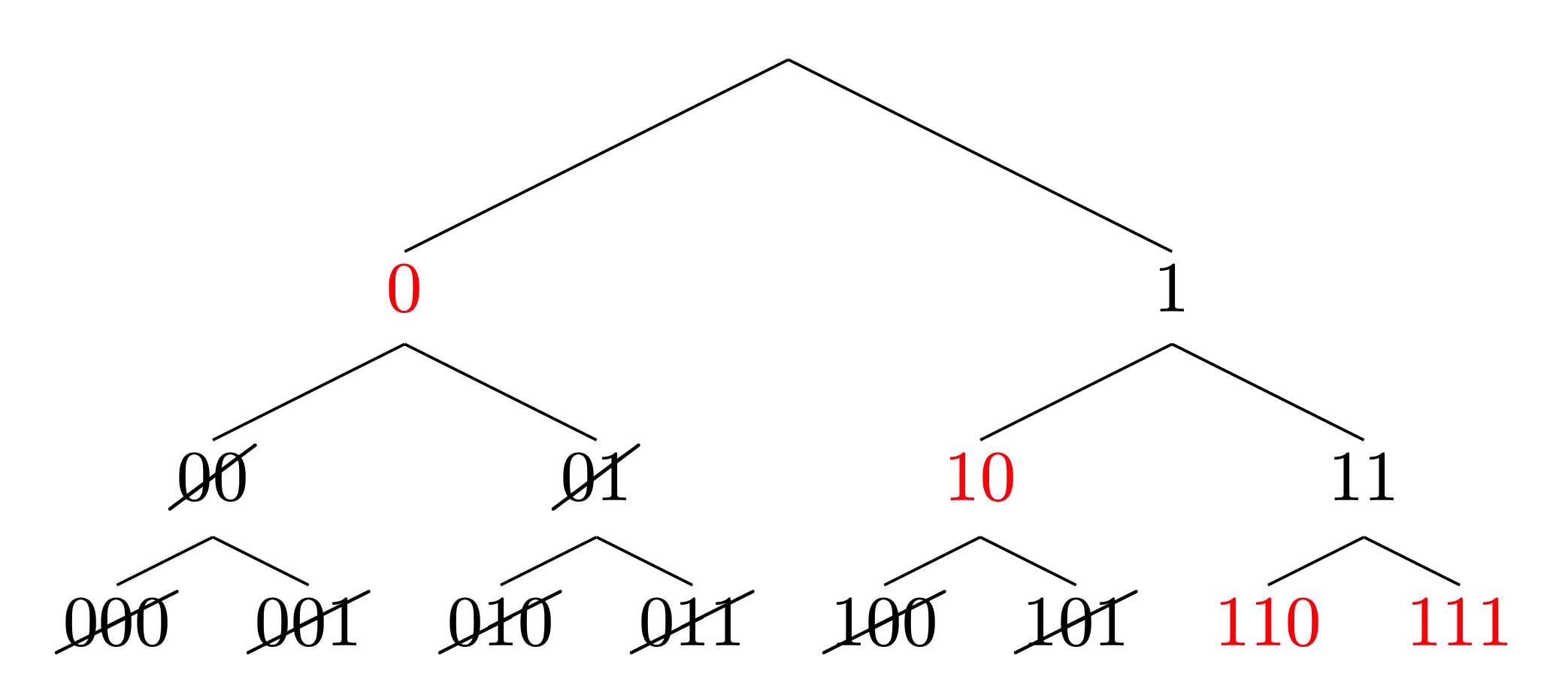
Figure 2. Construction of an instantaneous encoding
The red numbers are selected for codes. Note that one must not use the child nodes of a selected code. It is more efficient in transmission if we select a shorter code (less memory) for a frequently sent message.
How can we evaluate the efficiency of a code? The Shannon entropy arises from derivation of tight bound for this question.
Shannon entropy
We will use the Kraft-McMillan inequality without proving it. For someone who is interested, the proof can be found here.
Suppose that the messages at hand $\mathbf M=\{M_i\}_ {i=1}^m$ are sorted in descending order by their frequency. In addition, the more frequent its usage is, the shorter the encoded code becomes. That is,
\[p_1 \ge p_2 \ge \cdots \ge p_m, \\ \ell_1 \le \ell_2 \le \cdots \le \ell_m.\]The average length of the code is $\text{Avg}(\boldsymbol\ell) = \sum_{i=1}^m p_i \ell_i.$ Our goal is to find the minimal length of the average code length that satisfies the Kraft-McMillan inequality.
\[\begin{aligned} &\text{minimize }~ \text{Avg}(\boldsymbol\ell) \\ &\text{subject to }~ \sum_{i=1}^m 2^{-\ell_i} \le 1. \end{aligned}\]Simply applying Lagrangian method will solve the problem.
\[\mathcal L(\boldsymbol\ell) = \text{Avg}(\boldsymbol\ell) + \lambda\left(\sum_{i=1}^m 2^{-\ell_i} - 1\right) \\ \boldsymbol\ell^* = \argmin_{\boldsymbol\ell} \mathcal L(\boldsymbol\ell) \\ \ell_i^* \text{ is } \text{the solution of } \frac{\partial \mathcal L}{\partial \ell_i} = p_i - \lambda 2^{-\ell_i}\ln2 = 0.\]Since the solution is achieved at the equality condition of the K-M inequality,
\[\begin{aligned} 1 &= \sum_{i=1}^m p_i = \lambda \ln2 \sum_{i=1}^m 2^{-\ell_i^*} \\ &= \lambda\ln2 \end{aligned}\]So $\lambda$ should be $(\ln 2)^{-1}$ and $\ell_i^*$ should be $-\log_2 p_i$ so we get the minimal average code length of
\[\text{Avg}(\boldsymbol\ell^*) = \color{blue}{ -\sum_{i=1}^m p_i \log_2 p_i}.\]Similarly, the expectation of a random $\boldsymbol\ell^*$ becomes the definition of the Shannon entropy.
For a random variable $X$ with density function $p,$ the shannon entropy of $X$ is $$ \begin{aligned} H(X) &= -\sum_x p(x)\log_2 p(x) \\ &= \mathbb E \left[ \log\frac1{p(x)} \right] \label{shannon entropy}\end{aligned} $$
The term $ \log(1/p(x))$ can be interpreted as the amount of information in the sense that it gives more weight to $p(x)$ if it is less likely to happen. Hence in its definition, the Shannon entropy of a code $\mathbf X$ bounds the efficiency of all the possible codes of $\mathbf M$ from above.
In application, the entropy can be intuitively understand as an aggregated statistic of uniformity. Larger entropy implies the heterogeneity of the data $X_i.$ In communication system, more heterogeneous data implies inefficiency (every messages have the same frequency); In ecology, it implies an ecosystem of more species diversity; In thermodynamics, it can be seen as a generalization of the Boltzmann entropy.
References
- Shannon. 1948. A Mathematical Theory of Communication. Bell System Technical Journal. 27 (3): 379-423.
- The 12th KIAS CAC Summer School, Korea Institute for Advanced Study, Republic of Korea (the talk was given by Prof. Junghyo Jo at Seoul National Univerisity).
