$k$-mer Sequence Motif는 얼마나 자주 등장할까
전체 $n$ ntd로 이루어진 target RNA 한 가닥이 있다고 하자. 이 RNA는 완전히 랜덤하게 만들어진 가닥이라고 가정한다. 즉, 각 위치에 A, U, G, C가 같은 확률로 존재할 수 있다.
이제 $k$-mer sequence motif가 하나 있다고 하자. 이 sequence motif는 특정되어 있다.
이 때 Target RNA 가닥에서 이 motif가 한 번이라도 등장할 확률은 얼마일까?
분자생물학 연구실에서 생활하다 보면 종종 짧은 길이 시퀀스의 등장 가능성을 계산하고 싶을 때가 있다. 예를 들어, DNA/RNA를 가지고 하는 몇몇 실험에서 전 과정이 계획대로 진행되었는지 확인할 때, 특정 시퀀스 쿼리가 기대만큼 빈번히 등장하는지 계산해보면 (아주) 대강 감을 잡을 수 있다. (50nt마다 한 번 꼴로 빈번히 등장해야 할 쿼리가 1000nt를 살펴봐도 나타나지 않는다면 실험 어딘가에 문제가 있었던 것이라고 생각할 수 있다.)
그때마다 간단히 $k/4^n$으로 근사(?)하곤 했는데, 어느날 같은 연구실 친구가 “52nt 타겟에서 7nt 쿼리가 한 차례 이상 등장할 정확한 확률”이 궁금하다고 물어왔다.
막상 계산을 해보려니 생각보다는 복잡한 문제였다. 정확한 값은 지금껏 써왔던 방법과 얼마나 차이가 나는지, 또 52, 7이 아닌 일반적인 경우에도 적용할 수 있을지 궁금해져서 여사건의 확률 등의 기본적인 방법을 생각해보다 이런 기초중의 기초적인 방법으로는 풀리지 않는다는걸 알게 되었다.
검색을 해봐도 정확한 해답을 제시하는 사람은 많지 않았다 (너무 쉬운 문제여서 인지?). 여기서는 확률의 inclusion-exclusion principle을 이용한 해답을 소개하려 한다.
마주서기 문제
본 문제와 비슷하지만 비교적 단순한 문제를 먼저 살펴보자.
$n$쌍의 부부가 있다. 한 쪽에는 남편끼리, 다른 쪽에는 부인끼리 늘어 설 때, 적어도 한 쌍의 부부가 서로 마주보고 설 확률은 얼마일까?
이 문제 역시 여사건의 확률을 이용해서 풀기는 쉽지 않다 (재귀함수를 만들게 된다). 대신 inclusion-exclusion principle을 사용해서 풀어보자.
사건 $A_i$를 “i번째 부부가 서로 마주보고 서는 사건”이라고 하자. 그러면
\[P(A_i) = \dfrac{(n-1)!}{n!} \text{, } i=1, \cdots, n \\ P(A_i \cap A_j) = \dfrac{(n-2)!}{n!} \text{, } i < j \\ \vdots \\ P(A_1 \cap A_2 \cap \cdots \cap A_n) = \dfrac{1}{n!}\]이므로
\[\begin{aligned} P(\cup_{i=1}^{n} A_i) &= \sum_{i=1}^{n}P(A_i) - \sum_{i<j}P(A_i \cap A_j) \\ & + ... + (-1)^{n+1}\sum_{i<j<...<l}P(A_i \cap A_j \cap ... \cap A_l) \\ &= \sum_{i=1}^{n} (-1)^{i+1} \dfrac{1}{i!} \end{aligned}\]이다.
Sequence motif occurrence 문제
사건 $A_i \text{, } i=1, …, m$를 “i번째 위치에 motif가 등장하는 사건”이라고 하자. 단 $m$은 $n$을 $k$로 나눈 몫이다. 그러면
\[P(A_i) = \dfrac{4^{n-k}}{4^n} \text{, } i \leq n-(k-1) \\ P(A_i \cap A_j) = \dfrac{4^{n-2k}}{4^n} \text{, } i<j \text{ and } i, j \leq n-2(k-1) \\ P(A_i \cap A_j \cap A_k) = \dfrac{4^{n-3k}}{4^n} \text{, } i<j<k\text{ and } i, j, k \leq n-3(k-1) \\ \vdots \\ P(A_1 \cap A_2 \cap \cdots \cap A_m) = \dfrac{4^{n-mk}}{4^n}\]이므로 마주서기 문제에서와 같은 방법으로
\[P(\cup_{i=1}^{m} A_i) = \sum_{i=1}^{m} (-1)^{i+1} \binom{n-i(k-1)}{i} 4^{-ki}\]임을 알 수 있다.
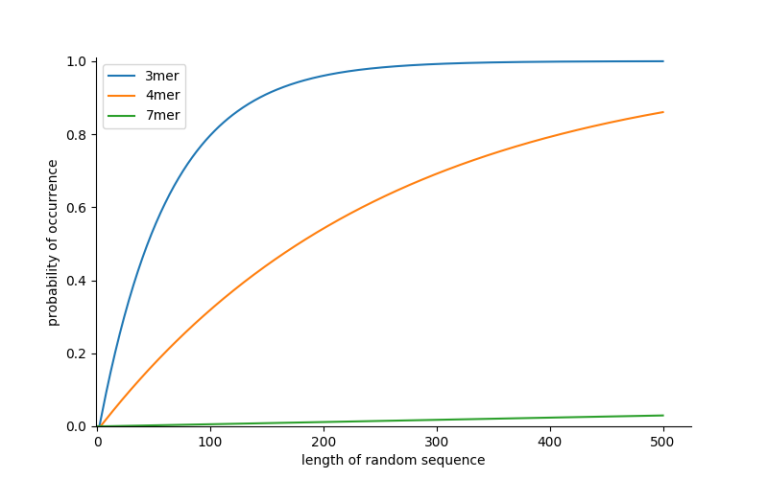
이 방법으로 1~500 ntd의 random target sequence에 3, 4, 7-mer fixed motif가 존재할 확률을 그래프로 나타내보면 다음과 같다.
Update:
위 방법이 일부 상황에서 정확한 값을 반환하지 않는다고 한다. 더 일반적인 경우에도 사용 가능한 Markov chain 방법을 쓴 Udaqueness 님의 글을 참고.
참고
- 위 방법을 구현한 스크립트를 공개해두었다.
- DFA라는 방식을 사용해서 해답을 제시한 글이 있다. 본 글에서 소개한 방법보다 일반적이고 우수한 방법인 듯하다.