3.2. Essential Techniques

Jul 8, 2021 • Sihyung Park
empirical process   asymptotics   Empirical Processes in M-estimation  

$\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}$ $\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}$

The part of the second necessity of the ULLN we would like to prove is the vanishing random entropy condition:

\[\frac1n H_{1,P_n}(\delta,\mathcal G) \overset P \to 0, ~ \forall \delta>0\]

which is weaker than the finite bracketing entropy condition. Together with the envelope condition, this implies the ULLN (theorem 3.7).

To prove this, I would like to introduce four techniques that are frequently used in this field and are directly used to prove the condition.

• 1. The chaining technique
  • Intuition
• 2. Maximal inequality for weighted sums
• 3. Symmetrization
  • Symmetrization of empirical processes
• 3. Hoeffding’s inequality

1. The chaining technique

The chaining technique allows one to approximate a totally bounded class $\mathcal G$ by some finite class. To be specific, suppose $\mathcal G = \{g_\theta:~ \theta\in\Theta\} \subset L^2(Q)$ and $\sup_{\theta\in\Theta}|g_\theta|_{2,Q} \le R < \infty.$ Since $\mathcal G$ is totally bounded, it has a minimal $\delta$-covering for any $\delta>0.$

To apply chaining argument, for $g_\theta \in \mathcal G$ and for $s=0,1,\cdots,$ let $\{g_j^s\}_ {j=1}^{N_s}$ be the minimal $R/2^s$-covering of $\mathcal G.$ Denote the best approximation of $g_\theta$ in each $R/2^s$-covering as $g_\theta^s.$ (i.e. $\|g_\theta-g_\theta^s\|_ {2,Q}\le R/2^s.$) Let $g^0_\theta \equiv 0.$ Then for any $S,$

\[g_\theta = \color{blue}{ \sum_{s=1}^S (g_\theta^{s}-g_\theta^{s-1}) } + \color{green}{ (g_\theta - g_\theta^s) } \tag{1}\]

The $L^2$-error from the green part approaches zero as $S$ becomes large. For fixed $S,$ the error from the blue part can be bounded since it is a finite sum.

Intuition

For intuitive understanding of what we have done here, consider the set of coverings.

\[\left\{ \{g_j^s\}_{j=1}^{N_s}:~ s=0,1,2,\cdots \right\}\]

The chaining technique approximates the “target” $g_\theta\in\mathcal G$ with “candidates” $g_\theta^s$ in each covering that becomes finer and finer as $s$ approaches infinity. That is, for fixed $g_\theta,$ the upper bound of $L^2$-error of approximation gets exponentially smaller.

\[\begin{aligned} \text{1. }&~ \sup_{1\le j\le N_0}\|g_\theta-g_j^0\|_{2,Q} \le R \\ \text{2. }&~ \sup_{1\le j\le N_1}\|g_\theta-g_j^1\|_{2,Q} \le \frac{R}{2} \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\ \text{S+1. }&~ \sup_{1\le j\le N_S}\|g_\theta-g_j^S\|_{2,Q} \le \frac{R}{2^S} \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \end{aligned}\]

Instead of merely approximating $g$ by $g^S_\theta$ with some large $S,$ we make an exact expression of it.

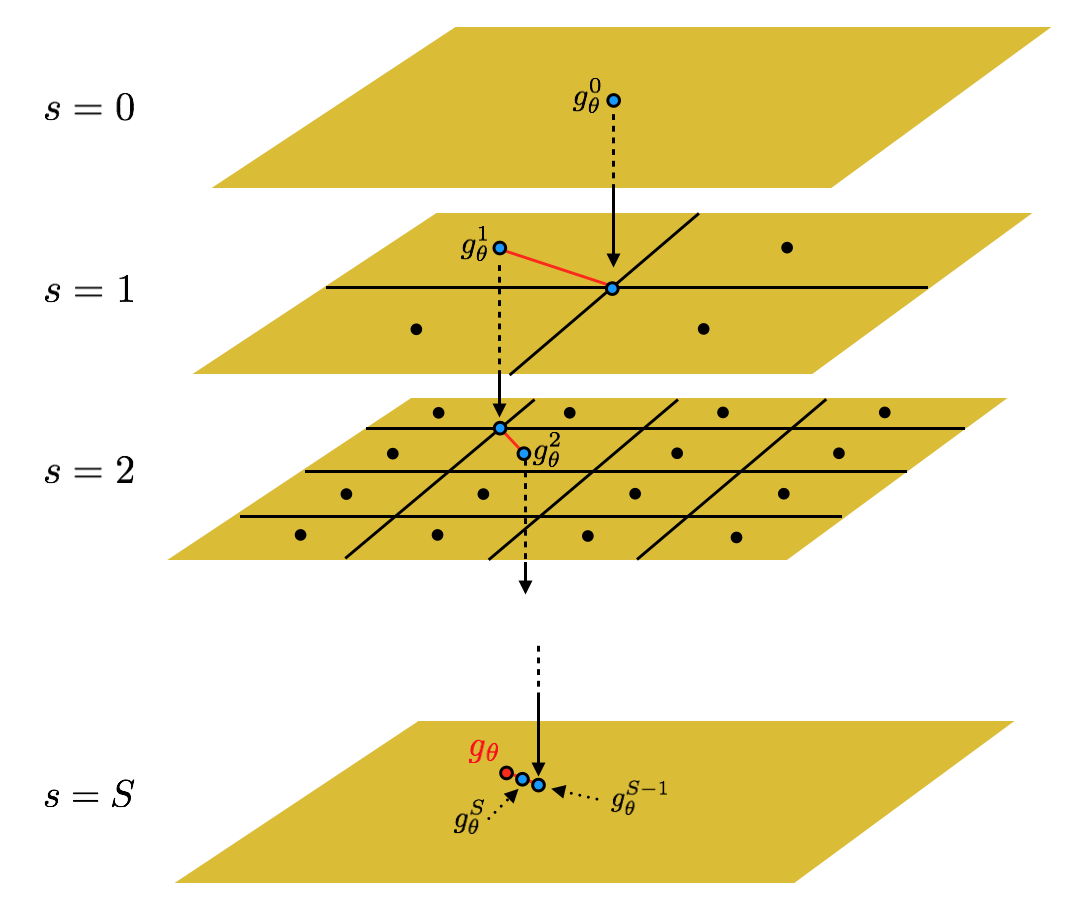
\[g_\theta = \sum_{s=1}^S (g_\theta^{s}-g_\theta^{s-1}) + (g_\theta - g_\theta^s)\]

van de Geer (2000) described this process as “following a path taking smaller and smaller steps.” Doing so allows us to get more precise bound by not generating additional error en route. Han Bao provides wonderful figure on the intuition of the technique (Figure 1).

Figure 1. The chaining technique (source: Han Bao's Blog)

2. Maximal inequality for weighted sums

The simplified version of the following maximal inequality will be used when proving the ULLN under vanishing random entropy condition. The full version will be used in chapter 5 and 8 of the textbook.

Let $\xi_1,\cdots,\xi_n \in \mathcal X$ be fixed points and $Q_n$ be the probability measure that has a mass of $1/n$ at each point $\xi_i.$ i.e.

\[Q_n = \frac1n \sum_{i=1}^n \delta_{\xi_i}\]

Let $W=(W_1,\cdots,W_n)\in\mathbb R^d$ be an $n$-dimensional random vector.

(a) For any $\gamma\in\mathbb R^n$ and $a>0,$ there exists some constants $C_1, C_2$ such that $$ \mathbb P\left( \left| W^\intercal \gamma \right| \ge a \right) \le C_1 \exp\left( -\frac{a^2}{C_2^2\|\gamma\|^2} \right). $$

(b) For some $R,$ $$ \sup_{g\in\mathcal G} \|g\|_{2,Q_n} \le R < \infty. $$

(c) For some $0\le\varepsilon<\delta, k>0$ there exists a constant $C$ depending only on $C_1$ and $C_2$ satisfying $$ C \left( \int_{\varepsilon/4K}^R H^{1/2}_{2,Q_n}(u, \mathcal G) du \vee R \right) \le \sqrt n (\delta - \varepsilon). $$

If (a)~(c) are satisfied, then $$ \mathbb P\left( \sup_{g\in\mathcal G}\left| \frac1n\sum_{i=1}^n W_ig(\xi_i) \right| \ge \delta,~ \frac1n\|W\|^2 \le K^2 \right) \le C \exp\left( -\frac{n(\delta-\varepsilon)^2}{C^2R^2} \right). $$

There are several remarks regarding the necessary conditions of the lemma. First, there is an intuition behind the requirement of the condition (a). Recall the Chernoff inequality for a subgaussian random variable:

\[\mathbb P\left( Z \ge a \right) \le \exp\left( -k a^2 \right) \text{ for some }k.\]

If $Z_i$ satisfies this inequality for all $i=1,\cdots,N,$ then the following maximal inequality holds¹.

\[\mathbb P\left(\max_{1\le i\le N} Z_i \ge a \right) \le \exp\left( \color{darkred}{ \log N } - ka^2 \right).\]

This implies that “it is the logarithm of the number of functions in a covering set that governs the behavior of empirical processes” (van de Geer, 2000).

Second, the condition (b), which implies totally boundedness of $\mathcal G,$ is for application of the chaining technique.

Finally, to successfully prove the lemma using the chaining technique, we need to bound the finite sum (blue part) of the expression (1). The sum of entropies generated from this part is \(\sum_{s=1}^S \frac{R}{2^s} \cdot H^{1/2}_{2,Q_n}(R/2^s, \mathcal G).\) Since the inequality^{2 3}

\[\sum_{s=1}^S \frac{R}{2^s} \cdot H^{1/2}_{2,Q_n}(R/2^s, \mathcal G) \le 2\int_{\rho/4}^R H^{1/2}_{2,Q_n}(u,\mathcal G)du\]

holds for $R>\rho$ and $S:=\min\{ s\ge1:~ R/2^s \le \rho \},$ we use the entropy integral condition instead of the sum condition for elegance.

expand proof

Only sketch of the proof will be presented here. The chaining technique plays the major role.Given $0\le\varepsilon<\delta,$ $k>0$ and $C>0$ that satisfies the condition (c). It suffices to show that of such $C,$ there exists the one that satisfies the condition (a).

Let $\{g_j^s\}_{j=1}^{N_s}$ be the minimal $R/2^s$-covering of $\mathcal G$ for $L^2(Q_n)$-norm. That is, $N_s = N_{2,Q_n}(R/2^s,\mathcal G).$ Let $g_\theta^s\in\{g_j^s\}_{j=1}^{N_s}$ so that $\|g_\theta-g_\theta^s\|_{2,Q_n}\le R/2^s.$ Let $$ S= \min\left\{ s\ge1:~ \frac R{2^s} \le \frac \varepsilon k \right\}. $$ Suppose that $\frac1n\|W\|^2 \le k^2,$ then $$ \begin{aligned} &\left| \frac1n \sum_{i=1}^n W_i(g_\theta(\xi_i)-g_\theta^s(\xi_i)) \right| \\ &\le \left( \frac1n\|W\|^2 \right)^{1/2} \cdot \left( \frac1n\sum_{i=1}^n(g_\theta(\xi_i)-g_\theta^s(\xi_i))^2 \right)^{1/2} \\ &\le k\cdot\|g_\theta-g_\theta^s\|_{2,Q_n} \\ &\le k\cdot\frac R{2^s} \le k\cdot \frac \varepsilon k = \varepsilon. \end{aligned} $$ The first inequality is from the Cauchy-Schwarz inequality. Using the result and the chaining technique, $$ \begin{aligned} &\mathbb P\left( \sup_{g\in\mathcal G}\left| \frac1n\sum_{i=1}^n W_ig(\xi_i) \right| \ge \delta,~ \frac1n\|W\|^2 \le K^2 \right) \\ &\le \mathbb P\left( \sup_{\theta\in\Theta}\left[\bigg| \frac1n\sum_{i=1}^n W_ig^s_\theta(\xi_i) \bigg| + \bigg| \frac1n\sum_{i=1}^n W_i(g_\theta(\xi_i)-g^s_\theta(\xi_i)) \bigg|\right] \ge \delta,~ \frac1n\|W\|^2 \le K^2 \right) \\ &\le \mathbb P\left( \sup_{\theta\in\Theta}\bigg| \frac1n\sum_{i=1}^n W_ig^s_\theta(\xi_i) \bigg| + \varepsilon \ge \delta\right) \;\;\;\;\;\;\;\;\;\text{(the previous result)} \\ &\le \mathbb P\left( \sup_{\theta\in\Theta}\bigg| \frac1n\sum_{i=1}^n W_ig^s_\theta(\xi_i) \bigg| \ge \delta-\varepsilon\right) \\ &\le \mathbb P\left( \sup_{\theta\in\Theta}\bigg| \frac1n\sum_{i=1}^n W_i(g^s_\theta(\xi_i) - g^{s-1}_\theta(\xi_i)) \bigg| \ge \delta-\varepsilon\right) \\ &\le \mathbb P\left( \sum_{s=1}^S \sup_{\theta\in\Theta}\bigg| \frac1n \sum_{i=1}^n W_i(g^s_\theta(\xi_i) - g^{s-1}_\theta(\xi_i)) \bigg| \ge \sum_{s=1}^S\eta_s(\delta-\varepsilon)\right) \\ &\le \sum_{s=1}^S \mathbb P\left( \sup_{\theta\in\Theta}\bigg| \frac1n \sum_{i=1}^nW_i(g^s_\theta(\xi_i) - g^{s-1}_\theta(\xi_i)) \bigg| \ge \eta_s(\delta-\varepsilon)\right) \\ &\le \sum_{s=1}^S N^2_{2,Q_n}(R/2^s,\mathcal G) \cdot \sup_{\theta\in\Theta} \mathbb P\left( \bigg| \frac1n \sum_{i=1}^nW_i(g^s_\theta(\xi_i) - g^{s-1}_\theta(\xi_i)) \bigg| \ge \eta_s(\delta-\varepsilon)\right) \\ &\le \sum_{s=1}^S e^{2H_{2,Q_n}(R/2^s,\mathcal G)} \cdot C_1 \exp\left( -\frac{n^2\eta_s^2(\delta-\varepsilon)^2}{C_2^2\sum_{i=1}^n(g_\theta^s(\xi_i)-g_\theta^{s-1}(\xi_i))^2} \right) \end{aligned} $$ for some $\eta_s>0$ for $s=1,\cdots,S$ such that $\sum_{s=1}^S\eta_s\le1.$

We need to find such $\eta_s$'s. Let $$ \eta_s = \frac{6C_2\cdot\frac{R}{2^s}\cdot H^{1/2}_{2,Q_n}(R/2^s,\mathcal G)}{\sqrt n(\delta-\varepsilon)} \vee \frac{\sqrt s}{8\cdot2^s} $$ then it satisfies the condition. Hence $$ \begin{aligned} &\mathbb P\left( \sup_{g\in\mathcal G}\left| \frac1n\sum_{i=1}^n W_ig(\xi_i) \right| \ge \delta,~ \frac1n\|W\|^2 \le K^2 \right) \\ &\le C_1\sum_{s=1}^S\exp\left( \frac{n(\delta-\varepsilon)^2\eta_s^2\cdot2^{2s}}{18C_2^2\cdot R^2}-\frac{n(\delta-\varepsilon)^2\eta_s^2\cdot2^{2s}}{9C_2^2\cdot R^2} \right) \\ &\le C \exp\left( -\frac{n(\delta-\varepsilon)^2}{C^2R^2} \right) \end{aligned} $$ where $$ C^2 = \max\{C_1^2,~ 18C_2^2\}. $$

3. Symmetrization

The symmetrization lemma allows us to apply the maximal inequality for weighted sums of random variables $X_i$’s. First, let \(X_1,\cdots,X_n,X_1',\cdots,X_n' \overset {\text{i.i.d.}} \sim P, \\ P_n=\frac1n\sum_{i=1}^n \delta_{X_i},~ P_n'=\frac1n\sum_{i=1}^n \delta_{X_i'}.\)

Suppose that for all $g \in \mathcal G,$ $$ \mathbb P\left( \bigg|\int g d(P_n-P)\bigg| > \frac\delta2 \right) \le \frac12 $$ Then $$ \mathbb P\left( \sup_{g\in\mathcal G} \bigg|\int g d(P_n-P)\bigg| > \delta \right) \le 2\mathbb P\left( \sup_{g\in\mathcal G} \bigg|\int g d(P_n-P_n')\bigg| > \frac\delta2 \right). $$

Note that for $\mathbb P\left( \big|\int g d(P_n-P)\big| > \delta/2 \right) > 1/2,$ the result is trivial. The name “symmetrization” comes from the $(P_n-P_n’)$ part (Such distribution is always symmetric).

expand proof

For simplicity, let $$ \mathbf X=(X_1,\cdots,X_n)^\intercal,~ \mathbf X'=(X_1',\cdots,X_n')^\intercal. $$ For $\delta>0$ that satisfies the given condition, let $$ A_g = \left\{ \mathbf X:~ \left|\int gd(P_n-P)\right| > \delta \right\},~ A = \bigcup_{g\in\mathcal G} A_g. $$ Define $g^*\equiv g^*(\mathbf X)$ so that $$ g^*(\mathbf X) = \begin{cases} g\in\mathcal G \text{ where } \mathbf X \in A_{g},& \mathbf X \in A \\ \text{any }g \in \mathcal G,& \mathbf X \notin A \end{cases} $$ Note that $g^*$ is independent to $P_n'.$ $$ \begin{aligned} &\mathbb P\left(A_{g^*},~ \bigg|\int g^* d(P_n'-P)\bigg| \le \frac \delta2 \right) \\ &= \mathbb E_\mathbf{X} \left[ \mathbf 1(A_{g^*}) \mathbb P\left(\bigg|\int g^* d(P_n'-P)\bigg| \le \frac \delta2 ~\bigg\vert~ \mathbf X \right) \right] \\ &\ge \frac12 \mathbb P(A_{g^*}) \\ &= \frac12 \mathbb P\left( \bigg|\int g^* d(P_n-P)\bigg| > \delta \right) \end{aligned}\tag{2} $$ Hence, $$ \begin{aligned} &\mathbb P\left( \sup_{g\in\mathcal G}\bigg|\int g~ d(P_n-P)\bigg| > \delta \right) \\ &\le \mathbb P\left( \bigg| \int g^*d(P_n-P) \bigg| > \delta \right) \\ &\le 2\mathbb P \left( \bigg| \int g^*d(P_n-P) \bigg| > \delta,~ \bigg| \int g^*d(P_n'-P) \bigg| \le \frac\delta2 \right) \\ &\le 2\mathbb P \left(\bigg| \int g^*d(P_n-P_n') \bigg| > \frac\delta2 \right) \\ &\le 2\mathbb P \left(\sup_{g\in\mathcal G}\bigg| \int g~d(P_n-P_n') \bigg| > \frac\delta2 \right). \end{aligned}\tag{$\because$ (2)} $$

Symmetrization of empirical processes

A random squence $(W_n)_{n=1}^\infty$ is Rademacher, if $W_i$'s are i.i.d. and $\mathbb P(W_1=1)=\mathbb P(W_1=-1)=1/2.$

Let $(W_n)_{i=1}^\infty$ be a Rademacher sequence that is independent to both $X_i$’s and $X_i’$’s. It is clear that

\[\left(g(X_i)-g_(X_i')\right) \overset d = W_i\left(g(X_i)-g(X_i')\right),~ \forall 1\le i\le n,~ \forall g\in\mathcal G\]

and

\[\begin{aligned} \int g~d(P_n-P_n') &= \frac1n\sum_{i=1}^n \left( g(X_i)-g(X_i') \right) \\ &\overset d= \frac1n\sum_{i=1}^n W_i\left( g(X_i)-g(X_i') \right). \end{aligned}\]

(1) $$ \mathbb P\left( \bigg| \int g~d(P_n-P) \bigg| > \frac\delta2 \right) \le \frac12,~ \forall g \in \mathcal G \\ \implies \mathbb P\left( \sup_{g\in\mathcal G} \bigg| \int g~d(P_n-P) \bigg| > \delta \right) \le 2 \mathbb P\left( \sup_{g\in\mathcal G} \bigg| \frac1n\sum_{i=1}^n W_i g(X_i) \bigg| > \frac\delta4 \right) $$

(2) $$ \exists R>0 \text{ such that } \sup_{g\in\mathcal G}\|g\|_{2,P}\le R \text{ and } \text{ for } n\ge8R^2/\delta^2 \\ \implies \mathbb P\left( \sup_{g\in\mathcal G} \bigg| \int g~d(P_n-P) \bigg| > \delta \right) \le 4 \mathbb P\left( \sup_{g\in\mathcal G} \bigg| \frac1n\sum_{i=1}^n W_i g(X_i) \bigg| > \frac\delta4 \right) $$

Only the result (1) will be proved. $$ \begin{aligned} &\mathbb P\left( \sup_{g\in\mathcal G} \bigg| \int g~d(P_n-P) \bigg| > \delta \right) \\ &\le 2 \mathbb P\left( \sup_{g\in\mathcal G} \bigg| \int g~d(P_n-P_n') \bigg| > \frac\delta2 \right) \\ &= 2 \mathbb P\left( \sup_{g\in\mathcal G} \bigg| \frac1n\sum_{i=1}^n W_i(g(X_i)-g(X_i')) \bigg| > \frac\delta2 \right) \\ &= 2 \mathbb P\left( \sup_{g\in\mathcal G} \bigg| \frac1n\sum_{i=1}^n W_ig(X_i) \bigg| + \sup_{g\in\mathcal G} \bigg| \frac1n\sum_{i=1}^n W_ig(X_i')\bigg| > \frac\delta2 \right) \\ &\le 2 \mathbb P\left( \sup_{g\in\mathcal G} \bigg| \frac1n\sum_{i=1}^n W_ig(X_i) \bigg| > \frac\delta4 \right). \end{aligned} $$

3. Hoeffding’s inequality

We will use the result without proving it.

Let $Z_1,\cdots,Z_n$ be independent random variables with $EZ_i=0$ for all $1\le i\le n.$ Suppose $b_i\le Z_i\le c_i$ for some $b_i<c_i$ for all $1\le i\le n.$ Then $$ \mathbb P\left( \sum_{i=1}^n Z_i \ge a \right) \le \exp\left( -2\frac{a^2}{\sum_{i=1}^n (c_i-b_i)^2} \right),~ \forall a>0. $$

References

• van de Geer. 2000. Empirical Processes in M-estimation. Cambridge University Press.
• Theory of Statistics II (Fall, 2020) @ Seoul National University, Republic of Korea (instructor: Prof. Jaeyong Lee).
• Han Bao’s Blog.

1. The proof is done easily by Jensen’s inequality and union bounds. ↩

2. The proof is direct from the fact that $H^{1/2}_{2,Q_n}(u,\mathcal G)$ is decreasing in $u$ and $\frac{R}{2^{S+2}} \le \frac{\rho}4 \le \frac{R}{2^{S+1}}.$ ↩

3. To define the integral at the right-hand side, without loss of generality, assume that $H_{2,Q_n}(\delta, \mathcal G)$ is continuous with respect to $u.$ (If this is not the case, then replace $H_{2,Q_n}(\delta, \mathcal G)$ by its smallest continuous majorant.) ↩