Batch Normalization 이해하기
Attention, residual connection 등 현대적인 딥러닝 모델을 디자인할 때 빠지지 않고 자주 쓰이는 테크닉들이 있다. 이번 글에서는 학습 과정에서 뉴럴넷을 안정시켜주는 표준화 기법 중 하나인 batch normalization에 대해 다뤄보겠다.
기존 방법의 문제점
BatchNorm이 어떤 의미를 가지는지를 알기 위해서는 BatchNorm이 고안되기 이전의 딥러닝 모형 초기화 및 학습 과정 표준화 과정을 둘러볼 필요가 있다.
뉴럴넷이 안정적으로 잘 학습되기 위해서는 입력층에 넣을 인풋과 각 층의 weight를 표준화할 필요가 있다. BatchNorm이 고안되기 전에는 두 가지 방법을 주로 사용했는데, 이전 포스트[1, 2]에서 각각의 방법을 간단히 다룬 바 있다. 간단히 복기하자면 이렇다: (1) 인풋은 centering과 scaling하고 (2) 인풋 뉴런 $n$개인 층의 weight를 $\div \sqrt{n/2}$로 표준화한다. 단순한 방법이지만 표준화하지 않은 입력, 가중치값을 사용했을 때에 비해 더 빨리, 더 좋은 성능으로 수렴하는 것을 경험적으로 확인할 수 있다.
여기서 중요한 문제가 발생한다. 입력층에 넣는 인풋은 표준화할 수 있다. 뉴럴넷에 넣기 전에 우리가 원하는 방식으로 원하는 만큼 preprocessing을 하면 된다. 그 결과 입력층의 input distribution은 항상 비슷한 형태로 유지가 되고 안정적으로 가중치 학습을 진행할 수 있다.

그러나 은닉층은 인풋의 분포가 학습이 진행됨에 따라 계속 변한다. 은닉층은 이전 레이어의 activation $f(XW)$을 입력으로 받는다. 학습 과정에서 가중치 $W$의 값이 $W^\prime$로 업데이트되면 이전 레이어의 activation 또한 $f(XW^\prime)$로 바뀌게 된다. 은닉층의 입장에서는 인풋 값의 분포가 계속 널뛰는 것이나 마찬가지이다. 입력 분포의 형태가 유지되지 않으므로 학습도 잘 진행되지 않는다. 그라디언트 값이 큰 학습 초기일수록 문제가 더 심각해진다.

Batch Normalization
알고리즘
바로 위에서 언급한 문제를 internal covariate shift라고 한다. 말 그대로 입력층보다 깊은, 즉 내부에 있는(internal) 층의 입력값, 즉 공변량(covariate)이 고정된 분포를 갖지 않고 이리저리 움직인다(shift)는 의미이다. BatchNorm은 바로 internal covariate shift를 해결하는 테크닉이다.
시도 1
은닉층의 입력도 표준화한다면 안정적으로 깊은 레이어의 가중치도 학습시킬 수 있을 것이다. “은닉층의 입력을 표준화한다”는 것은 곧 “이전 층의 출력(raw activation)을 표준화한다”는 의미와 같다.
딥러닝은 거의 항상 전체 샘플을 mini batch로 나누어 학습하고 가중치를 업데이트하므로 이전 층의 raw activation을 표준화할때도 각 batch마다 따로 표준화하면 된다.

이와 같이 각각의 minibatch의 평균 $\mu_{\mathcal{B}} = \frac{1}{m} \sum_i {x_iw_i}$과 표준편차 $\sigma_{\mathcal{B}} = \frac{1}{m} \sum_i {(x_iw_i - \mu_{\mathcal{B}})^2}$로 표준화한 activation $a_s = f(\frac{XW_1 - \mu_{\mathcal{B}}}{\sigma_{\mathcal{B}}})$를 은닉층 B의 입력으로 사용하면 은닉층 B의 입력은 고정된 분포를 따른다.
쉬워도 너무 쉽다. 이렇게만 하면 될 것 같지만..
시도 1의 문제점
문제가 몇 가지 있다. 이렇게 은닉층의 입력을 표준화하면 gradient update 과정에서 bias(편향)값이 무시된다. [시도 1]만을 사용해서 표준화한다고 할 때 그라디언트 업데이트 과정을 자세히 살펴보자. Raw activation을 $a_r = wx + b$라고 할 때 $E(a_r) = \frac{1}{n} \sum_i a_{r_{i}}$이므로
- 그라디언트를 계산한다.
- $\Delta b \propto - {\partial L}/{\partial b}$, where $L$ is a loss function.
- 편향(과 가중치)을 업데이트한다.
- $b \gets b + \Delta b$
- 편향을 업데이트한 이후의 raw activation은:
- $a_r ^\prime = wx + (b + \Delta b)$
- [시도 1]을 이용해서 센터링만 한 raw activation은:
- \[\begin{aligned} a_{r_{centered}} ^\prime &= a_r ^\prime - E(a_r ^\prime) \\ &= \{(wx + b) + \cancel{\Delta b}\} - \{ E[wx + b] + \cancel{\Delta b} \} \\ &= (wx + \cancel{b}) - E[wx + \cancel{b}] \end{aligned}\]
Bias $b$의 업데이트 $\Delta b$가 완벽하게 캔슬되었다. 초기 편향값에서 더 이상 업데이트가 되지 않는 것이다. 두 종류의 파라미터 $w$, $b$를 사용했는데 파라미터 $w$ 한 가지만 사용하는 단순한 모형으로 irreversible하게 변환된 것이다.
이 때문에 $b$ 대신 편향의 역할을 할 파라미터를 추가해야한다. 이 파라미터는 그라디언트 업데이트 과정에서 무시되어서는 안된다.
또 다른 문제도 있다. raw activation의 분포를 고정시키는 것은 좋지만 항상 $N(0, 1)$로 고정시킬 필요는 없다. 적절하게 scaling, shifting된 activation $\gamma \cdot \frac{a_r - \mu_{\mathcal{B}}}{\sigma_{\mathcal{B}}} + \beta$를 사용하는 것이 학습에 도움될 수도 있다.
이 형태의 activation을 사용할 경우 필요하다면 표준화를 되돌릴 수도 있다. $\gamma = \sigma_{\mathcal{B}}$, $\beta = \mu_{\mathcal{B}}$일 때 $\gamma \cdot \frac{a_r - \mu_{\mathcal{B}}}{\sigma_{\mathcal{B}}} + \beta = a_r$이기 때문이다.
시도 2
위의 문제를 극복하기 위해 표준화한 후 scaling 및 shifting 한 raw activation, 즉
\[a_\text{BN} = \gamma \cdot \frac{XW_1 - \mu_{\mathcal{B}}}{\sigma_{\mathcal{B}}} + \beta\]를 activation function $f$의 입력으로 사용한다. 은닉층 B의 입력으로는 $f(a_{BN})$을 사용한다. 이 방법을 BatchNorm이라고 한다. $\gamma$, $\beta$는 파라미터로 학습 과정에서 업데이트되는 값이다.
BatchNorm엔 장점이 꽤나 많은데,
- bias 업데이트를 무시하지 않는다. $\beta$가 bias처럼 행동한다. $\beta$값 업데이트는 표준화해도 캔슬되지 않는다.
- 은닉층마다 적절한 input distribution을 가질 수 있다. scaling factor $\gamma$와 shifting factor $\beta$를 사용해서 적절한 모양으로 입력분포를 조정할 수 있다.
- 필요한 경우 표준화를 하지 않을 수도 있다. 위에서 언급한 $\gamma = \sigma_{\mathcal{B}}$, $\beta = \mu_{\mathcal{B}}$의 경우이다.
- Activation 값을 적당한 크기로 유지하기 때문에 vanishing gradient 현상을 어느정도 막아준다. 덕분에 tanh, softmax같은 saturating nonlinearity를 사용해도 문제가 덜 생긴다.
- batch-wise로 계산하기 때문에 컴퓨팅하기 용이하다.
- 위의 장점들을 모두 가지면서, 동시에 각 층마다 입력 분포를 특정 형태로 안정시켜서 internal covariate shift를 방지할 수 있다.
- 입력 분포가 안정되므로 학습시 손실함수가 더 빨리, 더 좋은 값으로 수렴한다.
- 초기 learning rate를 크게 설정해도 안정적으로 수렴한다고 한다.
- Weak regularizer로도 작용한다고 한다.
이쯤 되면 거의 만능이다.
테스트할 때
지금까지 다룬 내용은 모두 학습 과정에서 일어나는 일들이다. 학습 과정에서는 raw activation을 minibatch mean, stdev로 표준화하면 됐었다. 그런데 학습을 마치고 테스트(또는 evaluation, inference)를 할 때에는 minibatch mean, stdev가 존재하지 않는다.
테스트 과정에서는 대신 전체 training data의 mean, stdev를 사용해서 BatchNorm을 한다. 이 때 전체 training data의 mean, stdev를 한 번에 계산하기에는 메모리의 제약이 있으므로, minibatch statistic을 평균낸 값을 대신 사용한다.
즉, $n$개의 minibatch가 있을 때,
\[\hat{\mu} = \frac{1}{n} \sum_i {\mu_{\mathcal{B}}^{(i)}} \\ \hat{\sigma} = \frac{1}{n} \sum_i {\sigma_{\mathcal{B}}^{(i)}}\]Minibatch statistic을 따로 저장할 필요 없이 학습 과정에서 moving average로 $\hat{\mu}$, $\hat{\sigma}$를 계산하면 된다. Exponential moving average를 사용해도 좋다.
$i$번째 minibatch statistic을 각각 $\mu_{\mathcal{B}}^{(i)}$, $\sigma_{\mathcal{B}}^{(i)}$라고 할 때,
\[\hat{\mu} \gets \alpha \hat{\mu} + (1-\alpha) \mu_{\mathcal{B}}^{(i)} \\ \hat{\sigma} \gets \alpha \hat{\sigma} + (1-\alpha) \sigma_{\mathcal{B}}^{(i)}\]BatchNorm layer
ReLU activation을 뉴럴넷의 레이어로 나타낼 수 있듯 BatchNorm 또한 레이어로 표현할 수 있다. BN layer는 raw activation과 activation function 사이에 위치한다. Convolutional layer에 BatchNorm을 적용하고 싶을 때에도 동일하게 raw feature map과 ReLU layer 사이에 BN layer를 추가하면 된다.
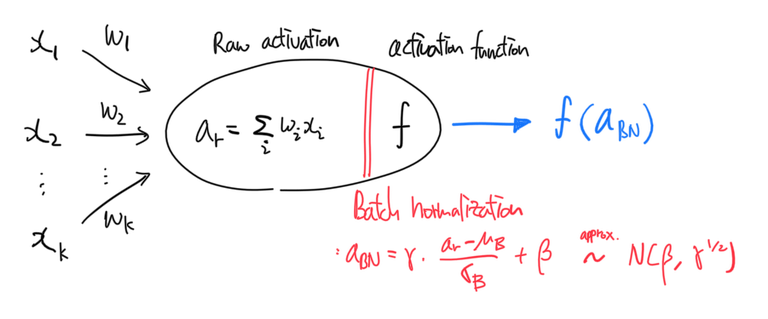
BN layer는 mini batch의 raw activations $a_r$를 입력받아 아래와 같은 연산을 수행하여 다음 레이어(activation function $f$)에 전달한다.
\[\text{BN}_{\gamma, \beta}(a_r) = \gamma \cdot \frac{a_r - \mu_{\mathcal{B}}}{\sigma_{\mathcal{B}}} + \beta\]또한 테스트 때 사용하기 위해 학습 과정에서 minibatch statistic의 exponential moving average(또는 그냥 MA)를 매 minibatch마다 업데이트한다.
TensorFlow 구현
구글에서 고안한 방법답게 TensorFlow에 이 내용들이 친절히 함수로 구현되어 있다. tf.nn.batch_normalization, tf.contrib.slim.batch_norm를 쓰면 간단히 위 알고리즘을 모형 구축에 사용할 수 있다.
tf.nn.batch_normalization을 사용할 경우, minibatch statistic의 EMA를 계산하는 코드를 따로 작성해야 한다.
tf.contrib.slim.batch_norm를 사용할 경우 is_training 옵션을 True로 주면 자동으로 EMA를 계산해서 저장하고, False로 주면 저장된 EMA 값으로 activation을 표준화한다.
TF-Slim 레이어에도 쉽게 적용시킬 수 있다.
import tensorflow as tf
import tensorflow.contrib.slim as slim
bn_params = {"decay": .9,
"updates_collections": None,
"is_training": tf.placeholder(tf.bool)}
net = slim.fully_connected(input, 1024,
normalizer_fn=slim.batch_norm,
normalizer_params=bn_params)
Convolutional layer에도 마찬가지다.
net = slim.conv2d(input, 64, [5,5], padding="SAME",
normalizer_fn=slim.batch_norm,
normalizer_params=bn_params)
업데이트
tf.slim 모듈이 TensorFlow 2.0 이후에서 deprecate되었다. 대신 TensorFlow core에 합류한 Keras를 사용하면 더 쉽게 모델 구축에 사용할 수 있다. tf.keras.layers.BatchNormalization을 다른 레이어와 마찬가지로 Sequential(), Functional() 혹은 직접 선언한 모델 서브클래스에 포함시키면 된다. Keras를 사용하면 .fit() 메소드를 호출하는 등, is_training=True인 경우와 .eval() 메소드를 호출하는 등 is_training=False인 경우가 자동으로 구별되어 알맞은 연산이 수행된다.
참고
- Ioffe and Szegedy, 2015, “Batch normlization: Accelerating deep network training by reducing internal covariate shift”
- TensorFlow API
tf.nn.batch_normalization()tf.contrib.slim.batch_norm()